Analyse de Dprime
1. Prenant le biais de réponse en compte
Le modèle de la performance de discrimination discuté dans le dossier précédent suppose que lorsque les auditeurs n'entendent pas de différence, ou ne sont pas sûrs, ils répondent « même » ou « différent » au hasard, de sorte que la performance est au hasard. Mais rien ne garantit que les auditeurs feront.
Supposons que vous étiez un sujet dans une tâche de discrimination et que vous vouliez montrer 100% la discrimination. Vous pouvez répondre à « différent » à chaque élément. et alors vous obtenez 100% déterminée en fonction du couple. Vous bien sûr également obtenir 0% correct sur les mêmes paires, parce que vous avez répondu « différent » à tous. Dans de nombreuses études, les mêmes paires ne sont pas analysées du tout, et cette stratégie de réponse fonctionnerait bien. Est-ce que ce résultat, 100% correct, signifie que vous discriminé les paires très bien? Il est clair que non; vous n'avez même pas avoir écoutés.
Le point est que% déterminée en fonction du paires seul n'est pas une mesure très significative de la discrimination. Il prend tout son sens quand elle est interprétée en termes de biais de réponse de l'auditeur. ou tendance à répondre « même » ou « différent ». Les réponses à la même paire peuvent être utilisés comme une indication de biais de réponse.
Ce système est également utilisé pour organiser et compiler les réponses des sujets. Autrement dit, le nombre (brut) de HITS etc. est entré dans les 4 cellules. Notez que si le nombre de stimuli du signal (différent) et pas de signal (SAME) sont les mêmes dans l'expérience, le nombre total de réponses dans la rangée supérieure sera égal au nombre total de la rangée inférieure (ou, plus généralement, le total de chaque rangée est connue à l'avance à partir de la conception de l'expérience); cependant, le nombre total de réponses dans la colonne de réponse OUI ne sera pas nécessairement le même que le nombre total dans la colonne de réponse NO, ni numéro peut être connu à l'avance. Mais, si vous connaissez le nombre de OUI et NON essais dans l'expérience, vous connaissez la valeur dans une colonne de la valeur dans l'autre. Par exemple. s'il y a 20 essais différents, et un sujet a 5 coups sûrs, alors ce sujet doit avoir 15 misses. Ainsi, seulement 2 des 4 chiffres dans le tableau (1 par ligne), ainsi que le nombre total d'essais, sont nécessaires pour caractériser la performance d'un sujet. Ce sont traditionnellement les Hits and fausses alarmes, et ceux-ci sont ensuite donnés en proportion des totaux des lignes, qui sont à leur tour considérés comme des estimations des probabilités de réponses:
le taux de réussite H. proportion des essais OUI à quel sujet OUI = P a répondu ( « oui » | OUI)
taux de fausses alarmes F. proportion de NO procès auquel sujet répondu oui = P ( « oui » | NO)
La table peut être réécrite avec ceux-ci et les 2 autres taux, avec un montant total de chaque rangée à 1,0; mais les résultats intéressants sont la paire (H, F). (Comparez ce à la proportion totale correcte, qui est (Hits +) / rejets Corriger toutes les réponses.)
Considérons alors que la performance du sujet est parfait (1,0), tandis qu'un sujet aléatoire a H = F et notre sujet qui répond toujours OUI a (1,1). Intuitivement, le meilleur sujet maximise H (et minimise ainsi le taux Mlle) et minimise F (et maximise ainsi le taux de rejet correct); et donc plus la différence entre H et F, la meilleure sensibilité du sujet. La statistique d »( « d-prime ») est une mesure de cette différence; il est la distance entre le signal et le bruit + signal. Cependant, d » est pas simplement H-F; au contraire, elle est la différence entre les transformées en Z de ces 2 Taux:
où ni H ni F peuvent être 0 ou 1 (le cas échéant, ajuster légèrement vers le haut ou vers le bas). Notez que les scores z peuvent être positives ou négatives, donc vous devez regarder les signes dans la soustraction.
Bien sûr, si vous utilisez les proportions d'origine ou leurs transformées, lorsque H = F, puis d « = 0. Cela est vrai si le taux « oui » est proche de 1 ou près de 0. Le plus haut possible d » (sensibilité maximale) est 6,93, la limite effective (en utilisant 0,99 et 0,01) 4,65, les valeurs typiques sont à 2,0, et 69% de réponses correctes pour les deux différents et mêmes essais correspond à ad » de 1,0.
Il existe d'autres mesures de sensibilité - par exemple une transformation autre que z (ou même transformer pas du tout), ou pondération différentielle de H et F, et même d'autres versions de d »(voir ci-dessous) - mais cela est celui que vous voyez habituellement dans la recherche de la parole.
3. Comment obtenir d » pour vos données.
Vous pouvez calculer H et F, les convertir en z-scores, et les soustraire. Le A5.1 de table M-C à l'annexe 5 donne les conversions z-score.
premier exemple de M-C d'obtenir H et F:
Ainsi, le taux de succès est H 20/25, ou .8
le taux de manque est 5/25 ou 0,2 (ces 2 ajouter jusqu'à 1,0)
le taux de fausse alarme est 10/25, ou 0,4
le taux de rejet est correct 15/25, ou 0,6 (ces deux ajouter jusqu'à 1,0)
et la paire (H, F) est (0,8, 0,4)
z (H) = 0,842 et z (F) = -0,253
d »= 0,824 - (- 0,253) = 1. 095
Colin Wilson a fourni sa formule Excel: d »= NORMINV (hit-débit, 0,1) - NORMINV (-taux de fausse alarme, 0,1)
où la NORMINV Excel « Renvoie l'inverse de la distribution normale cumulative pour la moyenne et l'écart type spécifié », 0 étant la moyenne spécifiée et 1 étant le SD spécifié.
Mais voir 13 ci-dessous pour les différents d » calculs pour différents modèles expérimentaux, y compris notre discrimination AX.
4. Une certaine utilisation de d » dans la littérature de discrimination.
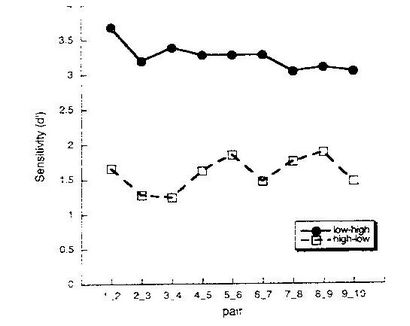
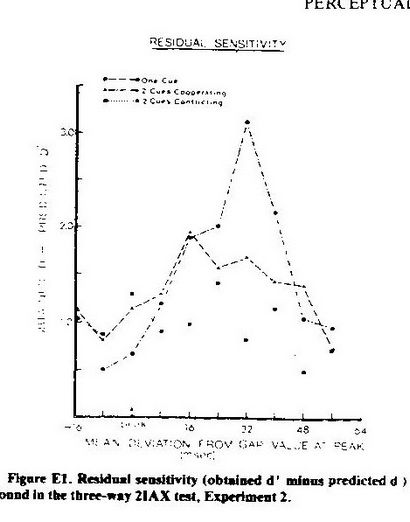
Parfois, H et CR sont ajoutés pour donner une proportion correcte (pour toutes les paires, et pas seulement pour les différentes paires), qui est ensuite transformé arcsin et analysé de la manière habituelle. Voir Sussman - Carney, Francis - Ciocca. Mais voir p.100ff M-C sur les dangers de la proportion correcte ( « une statistique inattendue chargée théorie »).
Bias est mesurée comme l'inclinaison du sujet à dire « oui » (ou « non »). La mesure de polarisation c est une fonction de H + F. Mais personne dans la recherche de la parole semble signaler, donc nous ne couvre pas comment le calculer.
6. Deux modèles de performance de discrimination AX
Quelle différence cela fera dans l'analyse d'une expérience? Considérons l'exemple de M-C dans (11) ci-dessus, pour le (0,8, 0,4) paire: d » est
1. 095. Cette paire se trouve sur p. 347 du tableau A5.4, avec un d » de 2,35. Comparez aussi les valeurs dans le fichier « un échantillon dprime.xls ». (Certaines valeurs doivent encore être regardé - essayez vous-même.) Les différences peuvent être importantes, mais il pourrait ne pas d'importance lorsque l'on compare les valeurs calculées par la même méthode.
7. L'application de la théorie de la détection des données d'identification
En effet, en soustrayant comme celui-ci, les réponses (par exemple, les / l / réponses) à un stimulus sont traités comme les HITS, et les réponses (avec la même catégorie de réponse) au stimulus suivant plus sont traités comme les faux ALARMES.
comparaison par paires de réponses d'identification est décrite par M-C pp. 212-13. Cependant, on ne sait pas qu'ils utiliseraient directement en tant que mesure de la distance de perception.
9. Certains Terminologie et modèles M-C
"One-intervalle discrimination": "un intervalle" désigne un stimulus à un essai; « Discrimination » signifie dire aux différents stimuli de l'expérience à part en sélectionnant des réponses différentes de l'ensemble disponible (non du procès!) - donc, prêter à confusion, cela fait référence à ce que nous appelons l'identification. Ce sont de 2 types:
- « Oui-non »: seulement 2 réponses sont disponibles; par exemple. pour chacun des stimuli, est-ce que vous avez vu avant (oui) ou non (non, c'est nouveau); est un Z (oui) ou non (non, c'est un Y). d » est calculé comme précédemment, bien que cela suppose qu'il y a un connu, correct, réponse pour chaque stimulus, ce qui est le cas pour l'identification des stimuli tirés d'un continuum.
- « Note »: plus de 2 réponses sont disponibles, sur une échelle, par exemple 1 à 5, où les 2 réponses de point de terminaison indiquent une grande certitude Voir pp M-C. 61ff. pour savoir comment calculer H et FA dans des expériences de notation. Voir aussi pp. 79ff des alternatives à la conception de notation, dans laquelle plusieurs conditions sont utilisées pour manipuler le biais.
« Deux intervalle »: 2 stimuli par essai
"2AFC": dont l'un de ces 2 stimuli? (Par exemple celui que vous avez vu avant (reconnaissance), que l'on est venu en premier (ordre temporel), lequel correspond à l'invite (identification))
M-C dire que la conception de 2AFC est mieux que oui aucune reconnaissance quand une connaissance a priori est un facteur de confusion probable; Mais parce que 2AFC est plus facile pour les sujets, d » est abaissée d'un facteur d'environ 0,7. Ils notent aussi que cette conception tend à minimiser les biais (au moins pour la présentation visuelle simultanée de paires de relance), pour cent correct est pas une mauvaise mesure de la sensibilité.