ARDL avec cointégration Bounds en utilisant EVIEWS 9 - Noman Arshed

Eh bien, nous pouvons maintenant avoir le module ARDL dans EViews 9 qui peut se répliquer mêmes résultats que par rapport à ce que Microfit peut faire avec l'avantage que nous pouvons avoir plus de deux retards et plus de 6 variables actuellement disponibles version de démonstration de Microfit ne permet pas. Vous pouvez télécharger la version d'essai de EViews 9 au lien suivant

Dans ce post, je vais donner un bref tutoriel sur la façon de faire ARDL dans EViews reste des détails peut être vu de mon précédent poste manuel ARDL.

Tout d'abord, nous devons importer les données dans les EViews 9

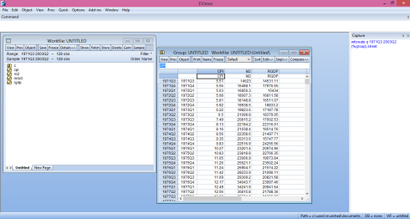
Après cela, nous sélectionnons les variables en appuyant sur le bouton de commande et la sélection des variables indépendantes première et variable dépendante après et clic droit et l'ouvrir comme équation. Ici, dans le menu déroulant, nous pouvons voir l'option de ARDL en bas

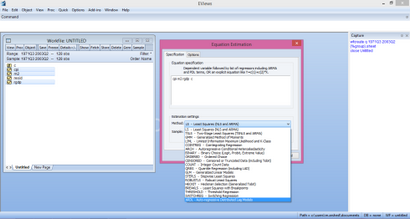
Sélectionnez-le. Il montrera les options de modèle ARDL

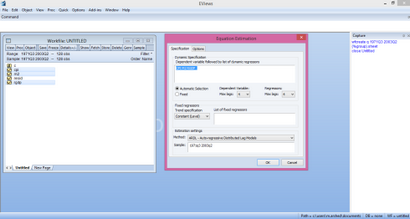
Ici, nous pouvons fixer un certain décalage particulier ou utiliser la sélection automatique dans les décalages maximales de variable et variable indépendante dépendante. Les critères de sélection de décalage automatique peuvent être modifiés de défaut dans la fenêtre d'option. Appuyez sur OK pour voir les résultats du modèle ARDL dans ce qui suit

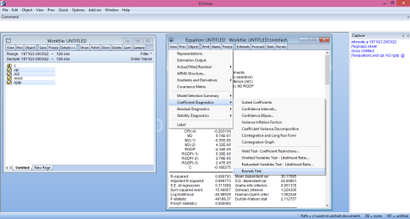
il montrera ensuite les résultats à court terme de et à long terme à la fois

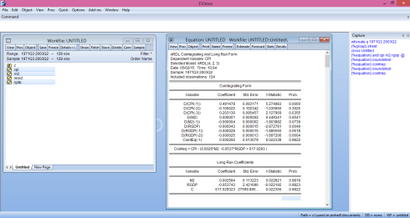
Ici, nous pouvons voir qu'il n'y avait pas cointégration parce que tous les longs coefficients d'exécution ne sont pas significatifs et le coefficient de cointEq (-1) est aussi qui non négatif et non significatif est avec les coefficients de court terme. Ceux-ci devraient être importants car ils sont importants. D'autres diagnostics comme hetroskedasticity, etc auto-corrélation peut être fait en sélectionnant les diagnostics de vue et les résidus.

Remarque: Vous pouvez générer Cusum ou CUSUM graphiques carrés à partir du lien suivant ou mettre à jour la version eviews.