Circuits en série simples, circuits série et parallèle, l'électronique des manuels scolaires
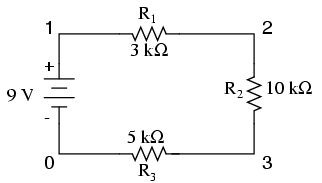
Commençons par un circuit en série constitué de trois résistances et une seule batterie:
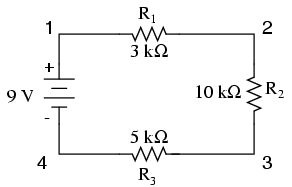

De la façon que la batterie de 9 volts est disposé, on peut dire que les électrons dans ce circuit couleront dans le sens inverse des aiguilles d'une montre, du point 4 à 3 à 2 à 1 et revenir à 4. Cependant, nous avons une source de tension et trois résistances. Comment pouvons-nous utiliser la loi d'Ohm ici?
Une mise en garde importante à la loi d'Ohm est que toutes les quantités (tension, courant, résistance et puissance) doivent se rapporter les uns aux autres en termes des mêmes deux points dans un circuit. Par exemple, avec une seule batterie, circuit unique résistance, on peut facilement calculer toute quantité, car ils sont tous appliqués aux mêmes deux points dans le circuit:
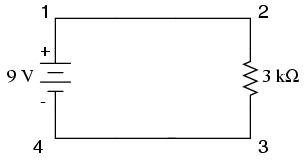

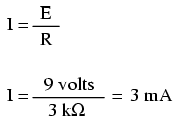
Comme les points 1 et 2 sont reliés entre eux avec du fil de résistance négligeable, tout comme les points 3 et 4, on peut dire que le point 1 est électriquement commune au point 2, et que le point 3 est électriquement commune au point 4. Puisque nous savons que nous avons 9 volts de force électromotrice entre les points 1 et 4 (directement à travers la batterie), et depuis le point 2 est commun aux points 1 et 3 commun au point 4, il faut aussi avoir 9 volts entre les points 2 et 3 (directement à travers la résistance ). Par conséquent, nous pouvons appliquer la loi d'Ohm (I = E / R) au courant à travers la résistance, parce que nous savons que la tension (E) à travers la résistance et la résistance (R) de cette résistance. Tous les termes (E, I, R) appliquent les mêmes deux points dans le circuit, à cette même résistance, afin que nous puissions utiliser la formule la loi d'Ohm sans réservation.
Cependant, dans les circuits contenant plus d'une résistance, il faut faire attention à la façon dont nous appliquons la loi d'Ohm. Dans l'exemple de circuit de trois résistances ci-dessous, nous savons que nous avons 9 volts entre les points 1 et 4, qui est la quantité de force électromotrice d'essayer de pousser les électrons à travers la combinaison en série de R1. R2. et R3. Cependant, nous ne pouvons pas prendre la valeur de 9 volts et le diviser par 3k, 10k ou 5k Ω pour essayer de trouver une valeur actuelle, parce que nous ne savons pas combien la tension est à travers une de ces résistances, individuellement.


Le chiffre de 9 volts est une quantité totale de l'ensemble du circuit, tandis que les chiffres de 3k, 10k, 5k et Ω sont des quantités individuelles pour les résistances individuelles. Si nous devions brancher un chiffre pour la tension totale dans l'équation d'une loi Ohm avec un chiffre pour la résistance individuelle, le résultat ne concernerait pas avec précision à toute quantité dans le circuit réel.
Pour R1. La loi d'Ohm concernera la quantité de tension aux bornes R1 avec le courant à travers R1. compte tenu de la résistance de R1, 3kΩ:
Mais, puisque nous ne connaissons pas la tension aux bornes R1 (uniquement la tension totale fournie par la batterie à travers la combinaison série de trois résistances) et nous ne savons pas le courant à travers R1. nous ne pouvons pas faire des calculs avec soit la formule. La même chose vaut pour R2 et R3. nous pouvons appliquer les équations de la loi de Ohm si et seulement si tous les termes sont représentatifs de leurs quantités respectives entre les deux mêmes points du circuit.
Alors, que pouvons-nous faire? Nous savons que la tension de la source (9 volts) appliquée à travers la combinaison série de R1. R2. et R3. et nous savons que les résistances de chaque résistance, mais étant donné que ces quantités ne sont pas dans le même contexte, nous ne pouvons pas utiliser la loi d'Ohm pour déterminer le courant de circuit. Si seulement nous savions ce que la résistance totale était pour le circuit: nous pourrions calculer le courant total avec notre chiffre pour la tension totale (I = E / R).
Cela nous amène au deuxième principe de circuits de la série: la résistance totale d'un circuit de série est égale à la somme des résistances individuelles. Cela devrait donner un sens intuitif: plus des résistances en série que les électrons doivent circuler à travers, plus il sera difficile pour les électrons de circuler. Dans le problème d'exemple, nous avons eu un 3 kQ, 10 kQ et la résistance 5 kQ en série, ce qui nous donne une résistance totale de 18 kQ:
Essentiellement, nous avons calculé la résistance équivalente de R1. R2. et R3 combinés. Sachant cela, on pourrait redessiner le circuit avec une seule résistance équivalente représentant la combinaison en série de R1. R2. et R3:
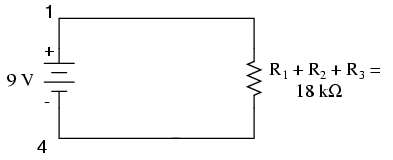

Maintenant, nous avons toutes les informations nécessaires pour calculer le courant de circuit, parce que nous avons la tension entre les points 1 et 4 (9 volts) et la résistance entre les points 1 et 4 (18 KQ):
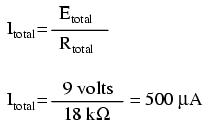

Sachant que le courant est égal à travers tous les composants d'un circuit en série (et nous avons déterminé le courant à travers la batterie), nous pouvons revenir à notre circuit d'origine schématique et notez le courant à travers chaque composant:
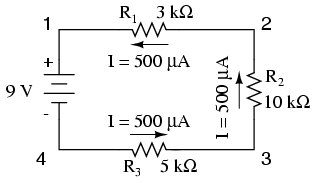

Maintenant que nous connaissons la quantité de courant à travers chaque résistance, on peut utiliser la loi d'Ohm pour déterminer la chute de tension dans chacune (application la loi d'Ohm dans son contexte):
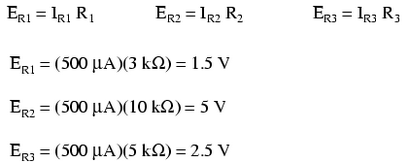
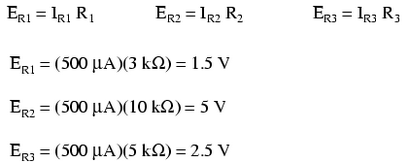
Remarquez que la tension chute à travers chaque résistance, et la façon dont la somme des chutes de tension (1,5 + 2,5 + 5) est égale à la batterie (alimentation) Tension: 9 volts. Ceci est le troisième principe des circuits de la série: que la tension d'alimentation est égale à la somme des chutes de tension individuelles.
Cependant, la méthode que nous venons d'utiliser pour analyser ce circuit de série simple peut être simplifié pour une meilleure compréhension. En utilisant une table à la liste toutes les tensions, les courants et les résistances dans le circuit, il devient très facile de voir qui de ces quantités peut être correctement lié dans l'équation de la loi toute Ohm:
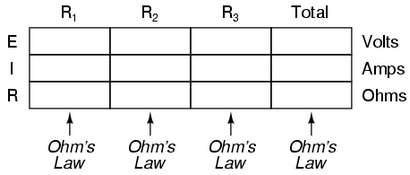

La règle avec une telle table est d'appliquer la loi d'Ohm seulement aux valeurs dans chaque colonne verticale. Par exemple, ER1 uniquement avec IR1 et R1; ER2 seulement avec IR2 et R2; etc. Vous commencez votre analyse en remplissant les éléments de la table qui vous sont données dès le début:
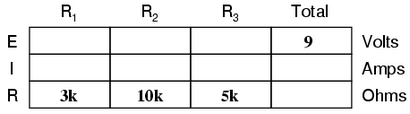

Comme vous pouvez le voir sur la disposition des données, nous ne pouvons pas appliquer les 9 volts de ET (tension totale) à l'une des résistances (R1. R2. Ou R3) dans la formule la loi de toute Ohm parce qu'ils sont dans des colonnes différentes . Les 9 volts de tension de la batterie ne sont pas appliquées directement à travers R1. R2. ou R3. Cependant, nous pouvons utiliser nos « règles » de circuits de la série pour remplir des taches blanches sur une ligne horizontale. Dans ce cas, on peut utiliser la règle de la série de résistances pour déterminer une résistance totale de la somme des résistances individuelles:
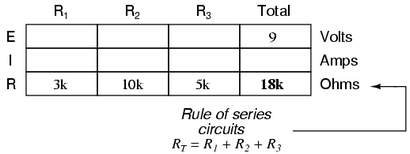

Maintenant, avec une valeur de résistance totale insérée dans la colonne de droite ( « Total »), nous pouvons appliquer la loi d'Ohm I = E / R à la tension totale et la résistance totale pour arriver à un courant total de 500 pA:
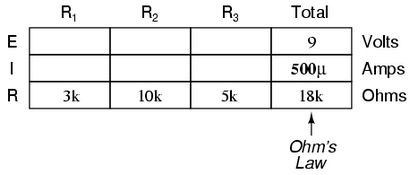

Ensuite, sachant que le courant est partagé à parts égales par tous les composants d'un circuit en série (une autre « règle » des circuits de la série), nous pouvons remplir les courants pour chaque résistance du chiffre actuel vient d'être calculée:
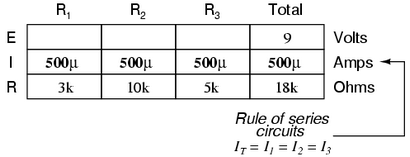

Enfin, nous pouvons utiliser la loi d'Ohm pour déterminer la chute de tension aux bornes de chaque résistance, une colonne à la fois:


Juste pour le plaisir, nous pouvons utiliser un ordinateur pour analyser automatiquement ce circuit même. Ce sera un bon moyen de vérifier nos calculs et devenir aussi plus familiers avec l'analyse informatique. Tout d'abord, nous devons décrire le circuit à l'ordinateur dans un format reconnaissable par le logiciel. Le programme SPICE nous allons utiliser exige que tous les points de placement électriquement uniques dans un circuit numérotés et composant est compris par lequel de ces points numérotés, ou « nœuds » qu'ils partagent. Pour plus de clarté, je numéroté les quatre coins de notre exemple circuit 1 à 4. SPICE, cependant, exige qu'il y ait un noeud zéro quelque part dans le circuit, donc je vais redessiner le circuit, la modification du système de numérotation légèrement:

Tout ce que je l'ai fait ici est renuméroté le coin inférieur gauche du circuit 0 au lieu de 4. Maintenant, je peux entrer plusieurs lignes de texte dans un fichier informatique décrivant le circuit en termes SPICE comprendront, avec quelques lignes de code supplémentaires diriger le programme pour afficher la tension et les données actuelles pour notre plus grand plaisir. Ce fichier informatique est connu sous le nom netlist dans la terminologie SPICE:
Maintenant, tout ce que je dois faire est de lancer le programme SPICE pour traiter la netlist et la sortie des résultats:
Cette impression nous dit la tension de la batterie est de 9 volts, et la chute de tension aux bornes de R 1. R 2. et R 3 sont 1,5 volts, 5 volts et 2,5 volts, respectivement. Les chutes de tension à travers l'un des composants dans SPICE sont référencées par les numéros de noeuds du composant se situe entre, de sorte que v (1,2) fait référence à la tension entre les noeuds 1 et 2 du circuit, qui sont les points entre lesquels R 1 est situé. L'ordre des numéros de noeud est important: lorsque SPICE émet un chiffre pour v (1,2), il considère la polarité de la même manière que si nous organisions un voltmètre avec le fil rouge sur le noeud 1 et le fil noir sur le noeud 2. Nous avons également un affichage montrant courant (quoique avec une valeur négative) à 0,5 milliampères ou 500 microampères. Ainsi, l'analyse mathématique a été justifiée par l'ordinateur. Ce chiffre apparaît comme un nombre négatif dans l'analyse SPICE, en raison d'une bizarrerie de la façon SPICE gère les calculs actuels.
- LA REVUE:
- Les composants d'une part de circuit série du même courant: ITOTAL = I1 = I2 =. Dans
- Résistance totale dans un circuit en série est égale à la somme des résistances individuelles: Rtotal = R1 + R2 +. rn
- tension totale dans un circuit en série est égale à la somme de la chute de tension individuelle: Etotal = E1 + E2 +. en
Essayez Law Calculator de notre Ohm dans notre section Outils.
← Prev Page IOU