Comment gérer Multicolinéarité dans MS-Excel et VBA - Finance et philosophie
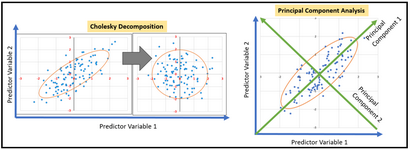
- Le problème avec multicolinéarité
Dans ce tutoriel, je vais vous montrer comment gérer Multicolinéarité dans MS-Excel wth l'aide de VBA. Un problème qui se pose souvent (et qui est souvent négligé dans les cours de 101 statistiques) tout en construisant des modèles de régression multivariée est le soi-disant multicolinéarité. Cette phenomen se produit lorsque l'on cherche à régresser une variable cible sur deux ou plusieurs variables prédictives corrélation croisée et peut provoquer le modèle de régression à se comporter l'une ou plusieurs des manières suivantes:
- un coefficient de régression qui est très important lors de la régression perd son importance dans le modèle multivarié
- les coefficients de régression se déchaîner: les variables prédictives qui eux-mêmes sont positivement (négativement) en corrélation avec la variable cible ont des coefficients négatifs (positifs). Ou si vous ajoutez ou soustrayez une variable prédictive les coefficients des autres variables prédictives fluctuent fortement.
- le modèle de régression montre des erreurs standard gonflés pour les coefficients.
Supposons que nous ayons l'ensemble suivant de 100 personnes:
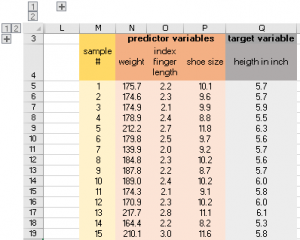
Nous voulons construire un modèle de régression pour prédire heigth en fonction des variables prédictives poids, la longueur de l'index et la taille chaussure. Nous sélectionnons donc la gamme S5: W9, entrez la formule:
et appuyez sur « shift » + « commande » + « enter »:
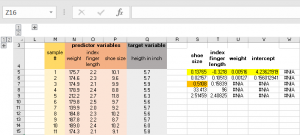
Les cellules jaunes mis en avant sont nos coefficients de régression, alors que la cellule d'orange en surbrillance fait référence à la r² de notre modèle.
Nous sommes intéressés à vérifier si notre modèle de régression souffre de multicolinéarité. Une façon de le faire est de calculer la variance que l'on appelle un facteur d'inflation (VIF). Nous pouvons calculer un VIF pour chacune de nos trois variables prédictives. Pour ce faire, nous régressons chaque variable prédictive sur les deux autres variables prédictives et calculer sa VIF respective avec la formule: 1 / (1-R²).
L'image suivante montre le calcul de la VIF (mis en évidence en bleu) de notre prédicteur poids variable.
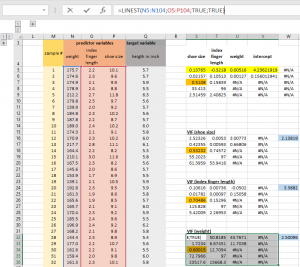
Nos VIFs sont modérément gonflés (VIF est 1 si les variables prédictives sont orthogonales, tandis que VIF> 10 est généralement considéré comme élevé), nous voulons donc rendre compte de la VIF gonflé dans notre modèle.
Tout d'abord, nous devons saisir la corrélation croisée entre les variables prédictives dans une matrice de corrélation (vous pouvez le faire soit avec la fonction de corrélation de l'analyse de données Excel ajouter ou en calculant la corrélation par paire des variables prédictives avec le fonction Excel: Correl) La matrice de corrélation montre des corrélations positives entre nos variables prédictives:
Avant de pouvoir appliquer notre matrice Cholesky nous avons d'abord besoin de normaliser nos données. Pour ce faire, nous devons calculer la moyenne et l'écart type pour chacune de nos trois colonnes de prédiction. Pour calculer la moyenne, nous utilisons la formule Excel MOYENNE alors que nous calculons l'écart-type avec la formule STDEV.S
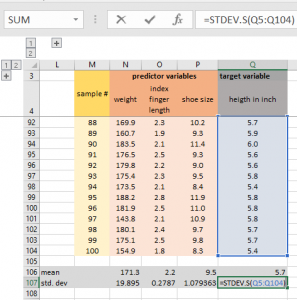
Nous standardisons alors nos prédictives et les variables cibles avec la fonction STANDARDIZE:
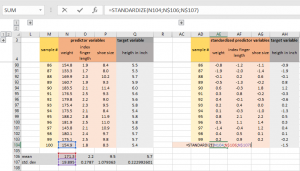
Nous allons vérifier s'il y a encore de corrélation croisée entre nos variables prédictives. Effectuer une deuxième analyse de corrélation nous permet de retrouver avec une matrice de corrélation ayant une identité (à savoir de corrélation croisée nulle):
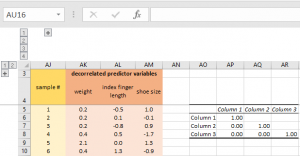
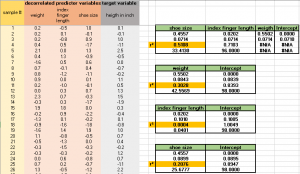
Il y a des choses importantes à emporter ici:
- poids comme premier prédicteur explique 30% de la variance de la variable cible et a une régression coefficient de 0,55, ce qui signifie une augmentation de poids de 0,55 écarts types provoque une augmentation de 1 écart-type dans notre hauteur variable cible.
- en plus de la première variable de prédiction notre deuxième longueur d'index de prédiction explique 0% de la variance de la variable cible et a une régression coefficient de 0,02, ce qui signifie une augmentation de la longueur de l'index de 0,02 écarts types provoque une augmentation de 1 écart-type dans notre hauteur variable cible.
- en plus de la première et deuxième prédicteur taille de chaussure de variable explique près de 21% de la variance de la variable cible et a une régression coefficient de 0,46, ce qui signifie une augmentation de la taille de la chaussure par 0,46 écarts types provoque une augmentation de 1 écart-type dans notre cibler hauteur variable.
3. Par conséquent, nous pouvons maintenant exprimer r² comme la somme de chacune des trois r² nos régressions univariées: 0,51 = 0,3 + 0 + 0,21. Il devient maintenant clair que l'on peut laisser tomber le longueur de l'index variable prédictive entièrement, car il contient presque aucune information concernant notre variable cible.
2. Option: blanchiment statistique en utilisant une analyse en composantes principales
D'un point de vue pratique, le grand avantage de l'ACP est que, en ne considérant que les vecteurs propres les plus importants (à savoir les composantes principales) vous pouvez réduire votre espace de fonction (à savoir le nombre de variables prédictives) énormément cinque presque pas de perte de r². Elle permet également d'ouvrir la porte à de nouvelles interprétations concering mécanismes de causalité sous-jacents qui sont capturés dans les composantes principales respectives. Maintenant passons à plonger dans la mise en œuvre effectivement PCA dans Excel.
Construire sur notre modèle de régression multivariée exemplaire en haut nous avons besoin à nouveau la matrice de corrélation des variables prédictives. Pour que notre PCA de travail, il est important de remplir également dans le triangle supérieur de notre matrice de corrélation. Maintenant, nous pouvons passer la matrice de corrélation comme une plage à la fonction de matrice
Les résultats de ces étapes se présentent comme suit:
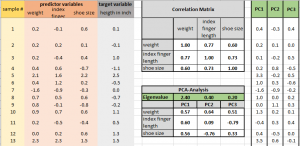
Notre première composante principale a une valeur propre de 2,40 capturant ainsi 2,40 / (2,40 + 0,40 + 0,20) = 80% de la variance de notre jeu de données d'entrée. La deuxième composante principale explique un supplément de 0,40 / (2,40 + 0,40 + 0,20) = 13,4% de la variance d'entrée-données.
Les 3 valeurs inférieures à la valeur propre 2,40 sont les soi-disant des charges pour chaque variable prédictive, qui est notre première combinaison principale est une combinaison linéaire des charges avec leurs valeurs d'échantillons respectifs. La première valeur de notre première composante principale est donc 0,57 * 175,7 + 0,60 * 2,2 + 0,56 * 10,1 = 183,5. Nous appliquons cette procédure à tous nos échantillons et aussi pour les deux autres composantes principales. Cela nous laisse avec un 100 x 3 matrice (indépendants / décorrélés) variables prédictives synthétiques. Nous régressons maintenant notre variable « en pouces heigth » cible (en utilisant la fonction de inbuild Excel LINEST) sur ces 3 variables qui nous laisse avec le résultat de la régression suivante.
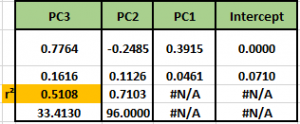
La valeur de r² 0,5108 est exactement le même que dans notre modèle de régression multivariée originale. Maintenant, nous allons nous laissons tomber 2 et 3 APC:
Le premier PC lui-même explique près de 37% de la variance dans la variable cible. Mais comment pouvons-nous interpréter PC1. Si nous regardons à nouveau notre PCA-table, nous reconnaissons immédiatement que toutes les charges pour PC1 sont positifs. Cela signifie qu'il est connecté positivement à nos trois variables prédictives qui sont tous capturer des mesure de la taille. Par conséquent, nous pourrions interpréter PC1 comme une mesure générale de taille qui (bien sûr) explique une grande partie de la variance dans notre cible heigth variable. Nous pourrions maintenant par exemple tracer l'équation de régression entre PC1 et notre variable cible facilement avec un tableau 2D en ligne.
Espérons que les différences entre les deux approches et leur mise en œuvre sont devenues suffisamment claire dans ce tutoriel. Les deux techniques de blanchiment statistiques empêchent de multicolinéarité occuting. En fonction du type de votre problème de régression et la tâche que vous voulez accomplir vous préférerez peut-être une technique de blanchiment statistique sur l'autre.
Alors que la transformation de blanchiment Cholesky vous laisse dans l'espace original et vous aide à évaluer la contribution respective supplémentaire de r² de chaque variable prédictive, PCA - par combinaison linéaire des variables prédictives - ouvre une nouvelle façon de trouver un mécanisme de causalité commun inhérent à la variables prédictives; en considérant uniquement les premiers éléments de k-principal, PCA vous permet également de réduire le nombre de variables prédictives énormément tout en ne perdant que de petites quantités d'information (r²) en ce qui concerne la variable cible.