Comment trouver le factoriel d'une fraction mathématiques Stack échange
D'après ce que je sais, la fonction factoriel est définie comme suit:
Et 0 $! = 1 $. Cependant, cette page semble dire que vous pouvez prendre le factoriel d'une fraction, comme, par exemple, $ \ frac! $, Qu'ils prétendent est égal à $ \ frac \ sqrt \ pi $ en raison de ce qu'on appelle la fonction gamma . De plus, ils commencent à obtenir le factoriel des nombres négatifs, comme $ - \ frac! = \ Sqrt $
Comment est-ce possible? Quelle est la définition de la factoriel d'une fraction? Qu'en est-il des nombres négatifs?
J'ai essayé des recherches sur Wikipédia et autres, mais il ne semble pas être une réponse claire.
La fonction gamma, représentée avec une capitale grecque gamma $ \ Gamma $, est une fonction qui étend la fonction factoriel à tous les nombres réels, à l'exception des entiers négatifs et zéro, pour lequel il n'est pas défini. $ \ Gamma (x) $ est liée à la factoriel en ce qu'il est égal à $ (x-1)! $. La fonction est définie comme
Il suffit d'utiliser pour calculer ce factorielles pour un certain nombre. Une façon pratique de calcul des fractions réelles avec dénominateurs même est la suivante:
Où n est un nombre entier. Mais gardez à l'esprit que la fonction gamma est en fait le factoriel de 1 inférieur au nombre qu'il évalue, donc si vous voulez $ \ frac! Utilisation de $ n = 2 au lieu de 1.
Ou, vous pouvez simplement mettre la fraction dans Google Calculator, qui utilise la fonction gamma pour évaluer factorielles d'un nombre quelconque.
Pour plus d'exemples de valeurs de la fonction gamma, voir ici.
(Si vous ne comprenez pas, ne vous inquiétez pas, parce que je ne soit, et l'article de Wikipedia sur la fonction semble manquer une définition claire de la ou comment elle se rapporte à $ \ sqrt $.)
Bien que la réponse sans aucun doute être Euler $ \ Gamma $ de, je me demandais toujours ce qui pourrait être une explnation plus intuitive pourquoi il en est ainsi.
Je pense, il est en quelque sorte plus compréhensible pour la fonction Beta étroitement lié et compte tenu de la formule impliquant sinus mentionné dans la réponse par neuguy ci-dessus.
Regardez $ \ sin (\ pi z) $. Ses zéros sont précisément tous les entiers. Voilà pourquoi il est périodique - il doit revenir à zéro à chaque entier, et exactement de la même manière que dans tout autre entier.
En fait, il y a une formule (I pense par Euler) $$ \ cdots (1- \ frac z) (1- \ frac z) (1- \ frac z) z (1- \ frac z1) (1- \ frac z2) (1- \ frac z3) \ cdots = \ frac1 \ pi \ sin (\ pi z) $$ reflète précisément.
Supposons maintenant que nous voulons savoir ce qui se passera si nous excluons $ 0 $, 1 $ $. $ N $ de l'ensemble des zéros. La fonction résultante restera zéro à tous les autres entiers, alors que dans l'intervalle $ -1 La façon dont tout cela se rapporte à factorielles et $ \ Gamma $ devrait être clair - on a $$ \ binom nz = \ frac, \ \ Gamma (x) = \ fracx $$ et $$ \ mathrm B (x, y) = \ frac. $$ En d'autres termes, 1 $ / \ Gamma (z) $ a des zéros précisément à des entiers non positif, de sorte que 1 / \ Gamma $ (kz) $ a des zéros précisément à k $ $, $ k + 1 $, $ k + 2 $. donc si nous voulons combiner ces derniers pour une fonction avec des zéros à tous les entiers sauf $ 0 $, $ 1 $. $ N $ nous devrions prendre $ \ frac1 $, ce qui se révèle être $ \ frac1 \ binom nz $. Une première idée qui vient à l'esprit pour définir le factoriel d'un nombre fractionnaire est interpolation: connaître les valeurs à deux nombres entiers successifs, les valeurs entre celles-ci doit être intermédiaire (regardant la « courbe », vous voyez qu'il est de plus en plus - très rapide - mais en douceur). Par exemple, vous pouvez estimer que 3,1 $! = 3! + 0,1 \ (4 fois! -3!) = 7,8 $.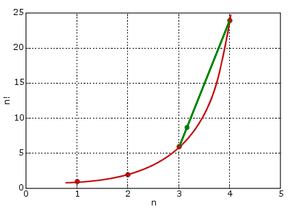
Cela ne semble pas très précis. En considérant les valeurs de $ \ En n! $, Vous voyez une tendance beaucoup plus proche d'une ligne droite.
Donc, pour une meilleure "précision", vous pouvez imaginer que la courbe est une exponentielle et faire l'interpolation sur les logarithmes:! $ \ Ln 3.1 = \ Dans 3 +0,1 (! \ En 4 - \ Dans 3) \ implique 3.1 ! = 6,8921 \ cdots $
Vous pouvez également augmenter le nombre de points utiliser pour l'interpolation, avec la formule lagrangien qui calcule un polynôme de degré supérieur.
Quoi qu'il en soit, cela est tout à fait empirique et ne conduit pas à une définition satisfaisante avec des propriétés intéressantes. Mathématiciens ont résolu différemment: ils ont trouvé des identités (! Telles que l'évaluation de l'intégrale $ \ int_0 ^ \ infty x ^ ne ^ dx = n $) qui peut être montré à l'égalité $ n $ lorsque n $ est un entier, et continuer à faire sens quand $ n $ est pas.
Ils ont donc commencé à utiliser cela comme une définition du factoriel
Avec cette formule, vous obtenez 3,1 $! = 6.812622863 \ cdots $
Extension des valeurs négatives est encore une autre histoire. Si l'on considère la définition récursive du factoriel, $ (n + 1)! = (N + 1) n! $, Ce qui permet de calculer des valeurs plus grandes et plus grandes, vous pouvez inverser comme $ (n-1)! = \ dfracn $. Aller en arrière, vous obtenez des points négatifs. Ensuite, vous aurez une surprise pour les entiers négatifs.