Comment trouver Probabilités Z avec le Z-Table
Vous pouvez utiliser le Z -table pour trouver un ensemble complet de probabilités « moins-que » pour une large gamme de z -values. Pour utiliser la table Z- pour trouver des probabilités pour un échantillon statistique avec une distribution normale (Z-), procédez comme suit:
Intersecter la rangée et de colonne des étapes 1 et 2.
Ce résultat représente p (Z < z ), the probability that the random variable Z is less than the value z (also known as the percentage of z -values that are less than the given z value ).
Par exemple, supposons que vous voulez trouver p (Z < 2.13). Using the Z -table below, find the row for 2.1 and the column for 0.03. Intersect that row and column to find the probability: 0.9834. Therefore p (Z < 2.13) = 0.9834.
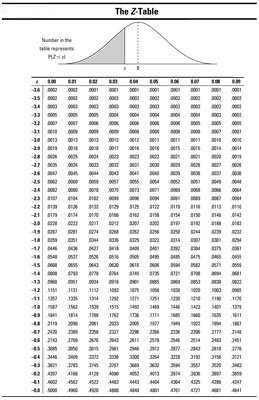
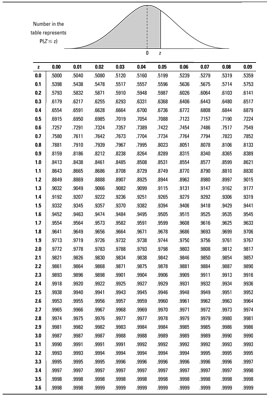
Constatant que l'aire totale sous la courbe normale quelconque (y compris la courbe normale standardisée) est de 1, il en résulte que p (Z < 2.13) + p (Z > 2,13) = 1. Par conséquent, p (Z> 2,13) = 1 - p (Z < 2.13) which equals 1 – 0.9834 which equals 0.0166.
Supposons que vous voulez chercher p (Z < –2.13). You find the row for –2.1 and the column for 0.03. Intersect the row and column and you find 0.0166; that means p (Z < –2.13)=0.0166. Observe that this happens to equal p (Z >+2,13) .La raison en est « parce que la distribution normale est symétrique. Ainsi la queue de la courbe ci-dessous représente -2,13 p (Z < –2.13) looks exactly like the tail above 2.13 representing p (Z > +2.13).