Comprendre translations, des réflexions et Rotations en géométrie, classe universelle
Comprendre translations, des réflexions et Rotations en géométrie
Après une compréhension de base de formes a commencé, il est impératif de prendre en compte les nombreuses façons dont ces formes peuvent alors être déplacés dans tout l'espace tout en conservant leurs caractéristiques d'origine. Comprendre que les formes qui ont été déplacés ne deviennent pas nécessairement de nouvelles formes, mais restent constantes dans une nouvelle position sur le plan qu'ils ont été placés est important. Il est à travers ce processus de compétences que l'on peut identifier les formes sont bien différentes et nouvelles et dont les formes ont tout simplement été déplacé vers une nouvelle position dans l'espace. Le processus de formes de transformation est une partie de symétrie.
Lors de l'examen des formes dans des espaces, il est impératif de répondre aux mouvements des formes de diverses manières. En règle générale, il sont considérés comme trois façons dont les formes peuvent être déplacées. Ces moyens sont les suivants: basculés, glissés ou transformés. La forme avant qu'elle ne soit déplacée de toute façon est connue comme la pré-image .La preimage devient l'image une fois que le mouvement se produit. Tant le preimage et l'image sont identiques dans tous les aspects, sauf pour les coordonnées dans l'espace existent.
Tout mouvement d'un objet peut être considéré comme une transformation. Comme chaque point de l'objet est considéré individuellement, la transformation des cartes chaque point individuellement et suit la façon dont chacun est déplacé ou changé. Dans le cas de la plupart des transformations, les points de l'objet sont suivis ou mis en correspondance sur la base du plan lui-même et toutes les longueurs reste constante. Isométrie est un terme utilisé pour faire référence à ces types de transformations. Il existe quatre types de isométriques qui sont: traductions, des rotations, des réflexions et des réflexions glissent. Il existe d'autres types de traductions, appelées dilatations, qui ne maintiennent pas les différentes longueurs.
Pavages peuvent démontrer une symétrie de réflexion. Un tessellation peut être dit avoir une symétrie de réflexion s'il y a un point dans la tessellation où le reflet de la tessellation originale peut être vu. La ligne où se produit cette réflexion est connu comme la ligne de miroir.
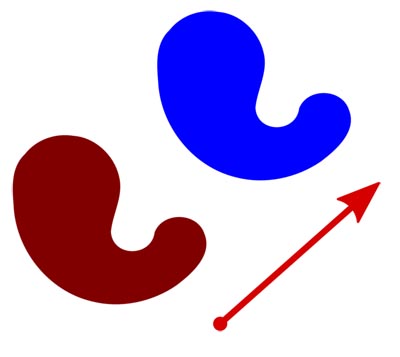
Quand une forme est glissé vers un nouvel emplacement dans l'espace, il est appelé une traduction. Les traductions sont ce que vous feriez si vous fait glisser une forme sur une table à votre partenaire. En examinant les points de l'objet, tous les déplacer dans la même direction pour la même distance. Il ne modifie pas l'ordre des points autour de l'objet. Pour qu'un mouvement soit une vraie traduction, l'objet doit être déplacé sans réflexion ou rotation de l'objet. Les traductions peuvent se produire dans un horizontalnature (à travers une ligne droite horizontale), une nature verticale (à travers une ligne droite verticale), ou dans une nature diagonale (sur une ligne droite en diagonale). Dans une translation, toutes les parties de la forme glissent dans le même sens et continuent de se déplacer à la même vitesse (couvrir la même quantité d'espace). Lorsqu'un objet a été traduit, il doit être déplacé dans une direction spécifique sur une distance spécifique. Par conséquent, toutes les traductions ont une certaine direction et la distance qui peut être décrit et mesuré.
Tous les pavages démontrent le concept de traduction. On pourrait dire que tous les pavages sont des motifs répétés et toutes les traductions vont créer une sorte de motif répété. Par conséquent, il peut être déduit logiquement que tous les pavages ont symétrie de translation.
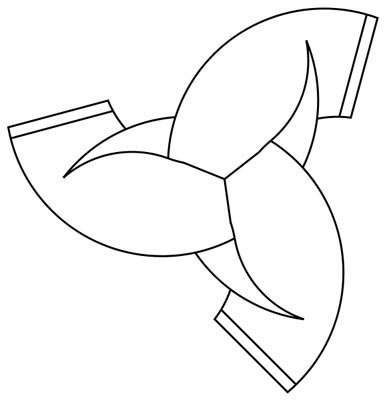
Quand une forme est tournée, il est appelé une rotation. Une rotation d'une forme se produit autour d'un point. La forme est déplacée au point par un nombre quelconque de degrés. Comme il se produit autour d'un point, chaque rotation a un centre et un angle. La rotation peut se produire dans un sens horaire ou antihoraire. Par conséquent, chaque rotation peut être décrite en termes de l'angle par lequel la rotation a eu lieu. Lorsqu'un objet est tourné cent quatre-vingts degrés ou à mi-chemin autour d'elle est appelée un demi-tour. Quand un objet est mis en rotation quatre vingt dix degrés ou d'un quart de tour, il est appelé à son tour comme Un quart. En examinant les rotations, le nombre de matches l'objet fera car il effectue une rotation est connue sous le nom de l'ordre. Il ne peut y avoir un ordre d'un, comme si l'objet nécessite une rotation complète pour aligner; il ne montre pas vraiment une symétrie de rotation.
Pour un tessellation être considéré comme ayant une symétrie de rotation doit représenter exactement le même que l'original tessellation après qu'il a été tourné. Si la tessellation fait en fait apparaître le même résultat que l'original après qu'il a été tourné, il peut être considéré comme un tessellation avec une symétrie de rotation.
Les formes peuvent être déplacées de plusieurs façons à un moment donné. Les objets peuvent être glissés et réfléchi. Une réflexion de glissement se produit quand une réflexion est associée à une traduction. Dans la réflexion de glissement, la traduction doit se produire le long de la ligne de réflexion ou d'une ligne de miroir. La réflexion de glissement est le seul type de symétrie qui comporte plus d'une étape.
Pour un tessellation pour démontrer glide symétrie de réflexion, la tessellation après la réflexion de glissement se produit doit montrer le même résultat que la tessellation d'origine avant la réflexion de glissement. Toute tessellation qui montre à la fois la symétrie de réflexion et symétrie de translation aura automatiquement glide symétrie de réflexion. Cependant, tous les pavages qui ont une symétrie de réflexion glide ne sont pas nécessairement symétrie par réflexion ou symétrie de translation.
Lors de l'enregistrement de toute forme de transformation, on va utiliser le système de coordonnées. Dans le système de coordonnées, les paires ordonnées sont utilisés pour représenter des points sur un graphique. Lorsque l'on regarde un graphique, l'axe horizontal est appelé l'axe x. Dans un ensemble de paires ordonnées, le premier nombre de la paire ordonnée se réfère au point x. Cela vous indique combien de places pour se déplacer horizontalement. L'axe vertical est appelé l'axe y. En paires ordonnées, le second nombre se réfère au point y. Cela vous indique combien d'espaces se déplacer verticalement. Par conséquent, le couple (6, 5) vous dira de se déplacer horizontalement (plus) six places et ensuite (verticalement) cinq places. L'espace que vous venez sur le graphique est l'endroit représenté par la paire ordonnée donnée. Il est par l'utilisation des couples que l'on peut décrire le placement d'objets sur un plan et plus tard, comment ils ont été transformés.