Des dizaines et des centaines se multiplient
Leçon 4.4: La multiplication des dizaines et des centaines
Un grand nombre comme le multiplicande: modélisation avec des matériaux de valeur de position.
La loi commutative nous aide lors de la première apprentissage de la multiplication de nombres à plusieurs chiffres. Il est plus facile de penser à 10x4 comme 4 séries de 10 que de 10 ensembles de 4:
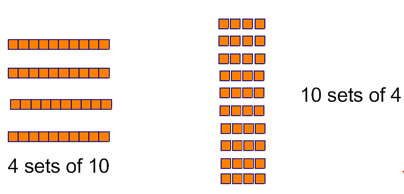
4 séries de 10 est mieux parce que nous groupons par 10 est dans notre système numérique, regroupant donc en ensembles de 10 est plus utile que le regroupement en ensembles de 4. Il est important de comprendre la valeur de lieu de comprendre cela, et il est aussi important de comprendre le commutative loi de multiplication, de sorte que vous pouvez interpréter les deux 4x10 et 10x4 en 4 groupes de 10.
Pour cette leçon, nous allons regarder les numéros où se multiplient un des numéros - que nous traiterons comme multiplicateur - est un nombre à un seul chiffre, et l'autre numéro - que nous traiterons comme multiplicande --s'agit un nombre 2 ou 3 chiffres.
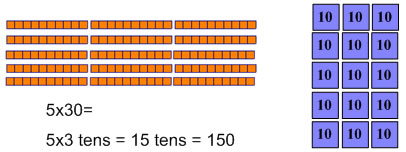
La première chose à apprendre est comment multiplier lorsque le multiplicande est un multiple de 10 ou 100. Nous allons commencer par montrer la multiplication en utilisant 10 matériaux de base. Ces diagrammes montrent 5x30 avec une proportionnelle (base 10 blocs) et un matériau non-proportionnelle (Montessori jeu de timbre). Dans les deux cas, 5 est le nombre de groupes, et il y a 30 dans chaque groupe.
Mettre ensemble: les algorithmes de multiplication
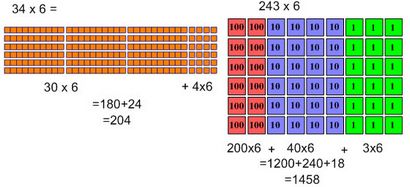
2 et numéros multiplier trois chiffres par un nombre à un seul chiffre peut être bien représenté en utilisant la loi distributive - penser à se multiplier dans chaque valeur de lieu, puis en ajoutant ces valeurs. Cela fonctionne bien avec une représentation avec manipulation:
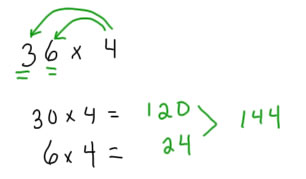
Les enfants, en cas de problème donné à un niveau qui est approprié pour eux, vont trouver des moyens de garder une trace des parties de problèmes comme ceux-ci. Van de Walle montre plusieurs de ces derniers sur la page 174. Toutes ces stratégies montrent une compréhension de la multiplication par les étudiants, et de montrer le développement du sens du nombre.
Les stratégies numériques complètes, et des stratégies de partitionnement du spectacle multiplicateur que l'enfant comprend que la multiplication peut être calculée par addition répétée, et que l'enfant a de bonnes stratégies de calcul mental pour ajouter un grand nombre.
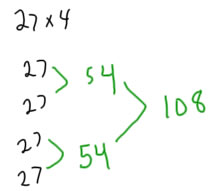
Les stratégies de rémunération à la page 175 montrent respectivement un undrestanding de la façon dont les multiplicateurs sont liés (loi distributive - à gauche), et comment réduire de moitié et sont doublement liés (un cas particulier de la multiplication et la division ou désagréger un facteur - associatif propriété ).
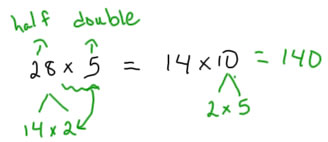
Toutes les idées importantes pour la multiplication peut être représenté par l'algorithme étendu. Dans cet algorithme, chacune des valeurs est place et on les écrit séparément, puis les produits partiels sont ajoutés. Dans cet algorithme, il est OK pour écrire les produits partiels dans un ordre quelconque, tant que vous avez tous.
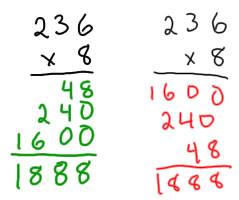
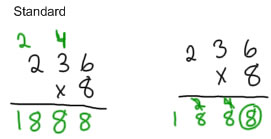
Quand et si vous enseignez l'algorithme standard, essayez de continuer à utiliser l'endroit langue de la valeur que vous appliquez quand on parle de nombres à plusieurs chiffres avec manipulation et addition et la soustraction: la deuxième multiplication n'est pas 8x3, il est 8x30 ou des dizaines 8x3, et quand vous portez les deux de 24 dizaines, ce n'est pas seulement 2, il est synonyme de deux cents.
L'algorithme de réseau est un moyen de réduire l'algorithme étendu où les nombres « carry » sont enregistrés dans un réseau que vous dessinez avant de commencer le problème, afin qu'ils restent organisés et finissent au bon endroit à la fin.
La partie la plus délicate de l'algorithme de réseau est que vous devez obtenir tout mis en place avec soin avant de commencer - vous avez besoin de vos chiffres espacés droite de sorte que vous pouvez adapter à un réseau (une boîte avec une diagonale tracée dans) en dessous de chaque chiffre. Puis, quand vous multipliez 8 par les chiffres en 236, les produits intègrent dans la zone sous le chiffre approprié et l'espacement du réseau se charge d'obtenir tout dans la bonne valeur de lieu.
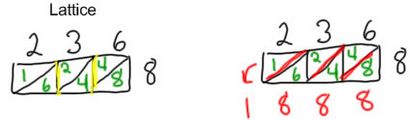
Lorsque vous multipliez les chiffres - les produits partiels, vous faites attention principalement sur les lignes du réseau descendant - les lignes de produits sous le chiffre que vous êtes en multipliant par. L'étape suivante consiste à ajouter - c'est où le « carry » chiffres sont ajoutés dans - et pour cette étape, vous faites attention aux lignes diagonales et les bosses chaque chiffre sur dans la valeur de bon endroit pour obtenir ajouté, et il finit par regarder un peu similaire à l'endroit où les chiffres portés se retrouvent dans la version anglaise de l'algorithme standard.