Différence Quotient, différence Quotient Exemples, Math @
Dans le calcul, nous étudions sur les fonctions. Une fonction est une relation bien définie qui a des valeurs de sortie fixe correspondant à certaines valeurs d'entrée. La valeur d'entrée est exprimée dans un graphique en tant que point. La différence entre les deux valeurs d'entrée est généralement nécessaire de calculer. Cette différence est notée $ \ delta $ (delta). Il est connu comme étant la différence dans le résultat de la fonction de deux valeurs. Cet écart est appelé comme différence de quotient. Le quotient de différence est utilisé dans le dérivé. Diviser la différence de fonction de la différence de point est appelé en tant que quotient de la différence. Il est par ailleurs connu comme le quotient de Newton. En termes numériques, on peut utiliser deux types de différences, on est égale différence et l'autre est la différence inégale.
La compétence de mettre en place et de simplifier quotients de différence est une aide nécessaire pour les étudiants de calcul. quotient de différence est utile pour trouver les formules générales des dérivés en calcul. Il est essentiel pour le calcul. Il tire son nom parce que les opérations en cause sont la soustraction et la division.
Supposons qu'il y ait une valeur d'entrée x et une autre est x + h, le quotient de différence est notée $ \ delta $ h. quotient de différence a son importance dans le calcul et d'autres branches des mathématiques. La formule du quotient de différence donne la pente de la sécante tracée à un point particulier de la fonction donnée. Dans cette page, nous allons en savoir plus en détail sur le quotient de différence, sa formule et ses différentes applications.
Différence Quotient Définition
Le quotient de différence est la pente de la droite tangente à un point sur le graphique d'une fonction donnée.
Soient X et Y sont les deux points distincts sur le graphe de la fonction f. Une ligne passant par les deux points X (x, f (x)) et Y ((x + h), f (x + h)), la formule pour trouver le quotient de différence est
Ceci est à partir du quotient de la différence que les formules de base pour les dérivés sont développés.
X et Y sont des points sur le graphe de f. Une ligne passant tout le chemin à travers les deux points X (x, f (x)) et Y (x + h, f (x + h)) est appelée une ligne sécante.
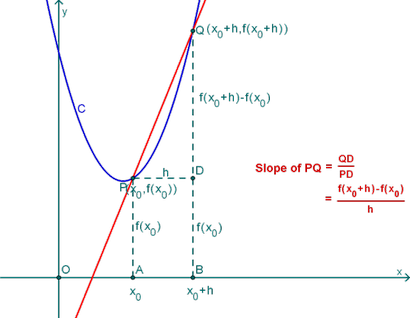
Interprétation de la Géométrique Quotient de différence:
Interprétation physique de différence Quotient:
Le taux moyen de changement dans le contexte du mouvement se réfère à la vitesse moyenne d'une particule en mouvement.
Soit f (t) représente la position d'une particule en mouvement dans le temps « t ». Si t1 et t2 sont deux instances de temps, les positions correspondantes de la particule est donnée par f (t1) et f (t2). Par conséquent, la différence f (t2) - f (t1) représente le déplacement de la particule dans l'intervalle t2 - t1. Ainsi, la différence quotient $ \ frac) - f (t _)> - t _> $ représente la vitesse moyenne de la particule dans l'intervalle t2 - t1.
Nous savons que la pente de la ligne par deux points (x, f (x)) et (x + h, f (x + h)) est m = $ \ frac - y_> - x _> $
Trouvez la différence Quotient
La différence Quotient est l'une parmi les formules importantes de calcul. Cela conduit à l'idée centrale de dérivés de calcul différentiel. Soit y une variable qui dépend d'une autre variable x. Nous y écrire en fonction de x que y = f (x). Laissez la valeur du changement x de x1 à x2. puis le changement de x, $ \ Delta $ x = x2 - x1 est appelé l'incrément de x. Les variations correspondantes de y sont y1 = f (x1) et y2 = f (x2) et l'incrément en Y est Ay = y2 - y1.
Le quotient de différence compare la variation ou incrément en Y pour le changement ou incrément de X.
Formule de différence Quotient
Cette variante est défini comme le quotient de la différence de f en x0 par « h » incrément et écrit$ \ Frac + h) - f (x _)> $
Cette formule peut être utilisée dans les programmes de solveur différents quotient prenant f (x). x0 et h comme entrées.
quotient différentiel peut donc être interprété comme étant le taux moyen de variation d'une fonction sur l'intervalle (x1. x2) ou sur l'intervalle de longueur « h ».
La formule de Fermat pour la différence Quotient pour un point général est $ \ frac $Étapes à suivre pour trouver le quotient de différence d'une fonction:
- Tout d'abord identifier la valeur de la fonction à x.
- Brancher x = x + h dans la fonction pour obtenir f (x + H)
- Trouver le résultat de la soustraction de f (x + h) - f (x)
- Diviser le résultat de la soustraction par h
Trouver la tangente à la courbe y = f (x) à (x0. Y0) à l'aide du quotient de différence
Le fait que la pente de la tangente est la limite du quotient de différence propose un procédé pour trouver la ligne tangente en utilisant la formule du quotient de différence.
- Calculer f (x0) et f (x0 + h)
- Calculer le quotient de différence.
- Calculer la pente en utilisant la formule, m = $ \ lim_ $ $ \ frac $
- Si la limite existe trouver la ligne tangente en utilisant la formule de point de pente. Si la limite n'existe pas la tangente est donnée par la ligne verticale x = x0.
résolu Exemple
Question: Trouver le quotient de différence à la fonction $ f (x) = x ^ $ à $ x = 2 $. En utilisant la limite du quotient de différence, trouver la pente de la tangente à $ x = 2 $.
Solution:
Question 4: Trouver le quotient de différence quand $ f (x) = 3x ^ - 2x + 1 $ et $ = 1 x 1 $, $ = 1,1 x 2 $
Solution:
Elucider valeurs données pour $ $ x 1 et x 2 $ $ dans l'équation, nous obtenons
$ F (x 1) = $ 2 et $ f (x 2 de) = 2,43 $ et $ x 2 - x 1 = 0,1 $
Par conséquent, le quotient de différence = $ \ frac) - f (t _)> - t _> = $ \ frac $ = 4,3 $ $
Différence Symmetric Quotient
La formule du quotient de la différence symétrique permet une meilleure approximation de la dérivée de la fonction que le quotient de la différence. Le quotient de différence de main gauche d'une fonction est $ \ frac $ où le point Q mobile est à la gauche du point fixe P. Lorsque le point Q approche P de droite droite quotient de différence de main est donnée par l'expression régulière $ \ frac $.Le quotient de la différence symétrique est le taux moyen de variation de la fonction dans l'intervalle (x - h, x + h). Il est aussi connu comme le quotient de la différence centrée autour de x. quotient de différence autour de x = Symmetric $ \ frac $
Il peut être vérifié. Le quotient de la différence symétrique est la moyenne des quotients de différence droit et gauche. quotient de différence Symétrique est également connu comme quotient de différence Centré que l'incrément est autorisé de chaque côté du point considéré et la moyenne est prise. Le quotient de la différence symétrique donne une meilleure approximation de f »(x) par rapport à la formule de Fermat.
Soit f (x) = x 2. Calculons le quotient de la différence en x = 2 et h = 0,01 en utilisant la formule de Fermat et la formule différence symétrique.
Différence Quotient en utilisant la formule de Fermat est $ \ frac - 2 ^)> = $ 4.01
quotient de différence en utilisant la formule de la différence symétrique est $ \ frac - 1,99 ^)> $ = 4
En utilisant la différenciation, on peut vérifier f »(2) = 4.
Différence Quotient d'une fonction
Le quotient de la différence d'une fonction f à tout point sur le graphe est donné par $ \ frac $. Parfois, nous pouvons utiliser Dx pour le changement de x et Dy pour le changement de y, alors nous avons $ \ triangle x = h $ et $ \ triangle y = f (x + \ triangle x) - f (x) $. Par conséquent, le quotient de la différence d'une fonction f devient $ \ frac $.résolu Exemple
Question: Trouver le quotient de différence de la fonction $ f (x) = 3x ^ + x - 1 $
Solution:
Limite de la différence Quotient
Par conséquent, le dérivé est la valeur limite du quotient de différence. En d'autres termes, la dérivée de la fonction x = x0 est donnée en,f »(x 0) = $ \ lim_ $ $ \ frac + h) - f (x _)> $.
Ainsi, le quotient de la différence constitue la base de la définition du dérivé qui est le thème central du calcul différentiel.
Alors que le quotient de différence calcule le taux moyen de variation d'une fonction, le dérivé donne le taux de variation instantané à un point, comme nous l'avons déjà vu dans la discussion des pentes des sécantes et de la tangente. De la même manière, en se référant à la fonction de position, tandis que le quotient de la différence se réfère à la vitesse moyenne de la particule se déplaçant dans un intervalle de temps donné, le dérivé se rapporte à la vitesse instantanée de la particule à un instant donné « t »$ V (t) = f »(t) = $ \ lim_ $ $ \ frac $
la formule du quotient de différence joue en tant que dérivé est défini pour être la limite du quotient de différence, une règle importante dans la recherche de la dérivée d'une fonction à l'aide des premiers principes.