Division (mathématiques)
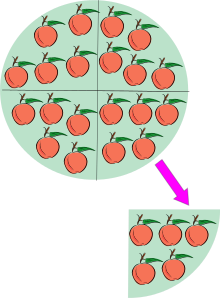
20 ÷ 5 = 4, parce que 20 les pommes contiennent cinq pommes quatre fois. C'est un exemple de division comme quotition plutôt que comme partition. On peut aussi dire que 20 ÷ 5 = 4 parce que quand 20 pommes sont divisées en 5 ensembles égaux de pommes, alors il y a 4 dans chacun de ces ensembles. C'est la division comme partition plutôt que comme quotition.
La division est l'une des quatre opérations de base de l'arithmétique. les autres étant plus. soustraction. et la multiplication. La division de deux nombres naturels est le processus de calcul du nombre de fois où un numéro est contenu dans une autre. [1]: 7 Par exemple, dans l'image à droite, les 20 pommes sont divisés en groupes de cinq pommes, et il existe quatre groupes, ce qui signifie que cinq peuvent être contenus dans les 20 quatre fois, ou 20 ÷ 5 = 4. la division peut également être considéré comme le processus d'évaluation d'une fraction. et notation fractionnelle (a / b et un /b) est couramment utilisée pour représenter la division. [2]
La division peut être considérée soit comme quotition ou partition. Dans quotition, 20 ÷ 5 signifie le nombre de 5s qui doivent être ajoutés pour obtenir 20. Dans partition, 20 ÷ 5 signifie que la taille de chacune des 5 parties dans lesquelles un ensemble de taille 20 est divisé.
La division est l'inverse de la multiplication; si a × b = c. alors a = c ÷ b. tant que b est non nul. Division par zéro est indéfini pour les nombres réels et la plupart des autres contextes, [3]: 246 parce que si b = 0. alors ne peut être déduit de b et c. comme alors c est toujours égal à zéro, indépendamment d'un. Dans certains contextes, division par zéro peut être définie, bien que dans une mesure limitée, et les limites impliquant la division d'un nombre réel tel qu'il se rapproche de zéro sont définies. [A] [2] [4]
En plus de la division des pommes, la division peut être appliquée à d'autres objets physiques et abstraits. Division a été définie dans plusieurs contextes, tels que les nombres réels et complexes et des contextes plus abstraits tels que des espaces vectoriels et les champs.
Division est souvent montrée en algèbre et de la science en plaçant le dividende sur le diviseur avec une ligne horizontale, appelée aussi une barre de fraction. entre eux. Par exemple, a divisé par b est écrit
Cela peut être lu à haute voix « a divisé par b », « a par b » ou « a sur b ». Une façon d'exprimer la division sur une seule ligne est d'écrire le dividende (ou numérateur), puis une barre oblique. puis le diviseur (ou dénominateur), comme ceci:
A mi-chemin de variation typographique entre ces deux formes utilise un solidus (fraction slash) mais élève le dividende, le diviseur et abaisse:
Chacune de ces formes peuvent être utilisées pour afficher une fraction. Une fraction est une expression de division où les deux dividende et le diviseur sont des nombres entiers (généralement appelé le numérateur et le dénominateur), et il n'y a pas d'incidence que la division doit être évaluée. Une deuxième façon de montrer division est d'utiliser le Obelus (ou signe de division), commun à l'arithmétique, de cette manière:
Cette forme est rare, sauf dans l'arithmétique élémentaire. ISO 80000-2 -9,6 indique qu'il ne doit pas être utilisé. Le Obelus est également utilisé seul pour représenter l'opération de division elle-même, comme par exemple une étiquette sur une clé d'une calculatrice.
Dans certaines cultures de -speaking non-anglais, "a divisé par b" est écrit un. b. Cette notation a été introduite en 1631 par William Oughtred dans son Clavis Mathematicae et popularisé plus tard par Gottfried Wilhelm Leibniz. [6] Cependant, dans l'usage anglais du côlon est limitée à l'expression de la notion connexe de rapports (puis « a est à b »).
Dans les classes élémentaires de certains pays, la notation b)
a> ou b) un ¯ >> est utilisé pour désigner un divisé par b. en particulier lors de la discussion division longue; De même, couramment utilisé en Amérique latine, b) _ >> pour la division courte (comme le montre un exemple sur cette page). [Citation nécessaire] Cette notation a été introduite par Michael Stifel dans Arithmetica integra. publié en 1544. [6]
Méthodes manuelles Modifier
Division est souvent introduit par la notion de « partage » un ensemble d'objets, par exemple un tas de bonbons, en plusieurs parties égales. Distribuer les objets plusieurs à la fois dans chaque cycle de partage de chaque partie conduit à l'idée de « segmentation », division à-dire par soustraction répétée.
Une personne peut calculer la division avec un abaque en plaçant de façon répétée le dividende sur l'abaque, puis en soustrayant le diviseur le décalage de chaque chiffre du résultat, en comptant le nombre de divisions possible à chaque décalage.
Une personne peut utiliser des tables de logarithmes pour diviser deux nombres, en soustrayant les logarithmes des deux chiffres, puis regardant l'antilogarithme du résultat.
Par ordinateur ou avec l'assistance informatique Modifier
Les ordinateurs modernes calculent la division par des méthodes qui sont plus rapides que la division longue: voir algorithme de division.
Dans l'arithmétique modulaire. certains chiffres ont un inverse multiplicatif par rapport au module. Nous pouvons calculer la division par multiplication dans un tel cas. Cette approche est utile dans les ordinateurs qui ne disposent pas d'une instruction de division rapide.
Division est droit distributive sur l'addition et la soustraction. Cela signifie:
de la même manière que dans la multiplication (a + b) × × c = a + b × c c. Mais la division n'est pas gauche distributive, à savoir que nous avons
S'il y a plusieurs divisions dans une rangée l'ordre de fonctionnement va de gauche à droite [7] [8]:
La division euclidienne est la formulation mathématique de l'issue du processus habituel de la division des nombres entiers. Il affirme que, deux nombres entiers, a. le dividende. et B. le diviseur. de telle sorte que b ≠ 0, il y a des nombres entiers q unique. le quotient. et r. le reste, de telle sorte que a = bq + r et 0 ≤ r < | b |, where | b | denotes the absolute value of b .
Division des entiers n'est pas fermée. Mis à part la division par zéro étant non défini, le quotient est un nombre entier pas moins que le dividende est un multiple entier du diviseur. Par exemple, 26 ne peut pas être divisé par 11 pour donner un entier. Un tel cas utilise l'une des cinq approches:
Entiers dans un divisant programme informatique nécessite une attention particulière. Certains langages de programmation. comme C. traiter division entière comme dans le cas 5 ci-dessus, si la réponse est un nombre entier. D'autres langues, comme Matlab et chaque système d'algèbre informatique renvoient un nombre rationnel comme la réponse, comme dans le cas 3 ci-dessus. Ces langues offrent également des fonctions pour obtenir les résultats des autres cas, soit directement, soit à partir du résultat de cas 3.
les règles de divisibilité peuvent parfois être utilisées pour déterminer rapidement si un entier divise exactement dans une autre.
Le nombre de rationnel Modifier
Le résultat de la division deux nombres rationnels est un nombre rationnel lorsque le diviseur est de 0. La division de deux nombres rationnels p / q et r / s peut être calculé comme
Division de deux nombres réels résultats dans un autre numéro réel lorsque le diviseur est de 0. Il est défini un / b = c si et seulement si a = cb et b ≠ 0.
Division d'un nombre par zéro (où le diviseur est égal à zéro) est indéfini. En effet, zéro multiplié par un nombre fini aboutit toujours à un produit de zéro. Entrée d'une telle expression dans la plupart des calculatrices produit un message d'erreur.
La division de deux nombres complexes des résultats dans un autre nombre complexe lorsque le diviseur est différent de 0, qui est trouvé avec le conjugué du dénominateur:
Division des nombres complexes exprimés sous forme polaire est plus simple que la définition ci-dessus:
On peut définir l'opération de division pour polynômes en une variable sur un champ. Puis, comme dans le cas des entiers, on a un reste. Voir division euclidienne des polynômes. et, pour le calcul écrit à la main, longue division polynomiale ou division synthétique.
division gauche et à droite Modifier
Parce que la multiplication de matrices n'est pas commutative. on peut également définir une division gauche ou soi-disant anti-slash-division comme A \ B = A -1 B. Pour que cela soit bien défini, B -1 nécessité de ne pas exister, mais un -1 n'a pas besoin d'exister. Pour éviter toute confusion, la division telle que définie par A / B = AB -1 est parfois appelée division de droite ou une barre oblique-division dans ce contexte.
Notez qu'avec la division gauche et à droite Selon cette définition, A / (BC) est en général pas les mêmes que (A / B) / C et ni est (AB) \ C le même que A \ (B \ C). mais A / (BC) = (A / C) / B et (AB) \ C = B \ (A \ C).
Modifier pseudoinverse
Pour éviter les problèmes lorsque A-1 et / ou B -1 n'existent pas, la division peut également être définie comme la multiplication avec la pseudo. à-dire A / B = AB + et A \ B = A + B. où A + et B + désigne la pseudo de A et B.
En algèbre abstraite. étant donné un magma avec * de l'opération binaire (qui pourrait théoriquement être appelée multiplication), division gauche de b par un (écrit a \ b) est généralement définie comme étant la solution x à l'équation x = a * b. si celle-ci existe et est unique. De même, la division droite de b par un (écrit b / a) est la solution de l'équation y pour y * a = b. Division en ce sens ne nécessite pas * d'avoir des propriétés particulières (telles que commutativité, associativité, ou un élément d'identité).
Le dérivé du quotient de deux fonctions est donnée par la règle du quotient: