ferromagnétique accordable température ambiante en utilisant un oxyde de fer et d'oxyde de graphène nanocomposite,
introduction
Manipulant les propriétés d'un matériau ferromagnétique par des moyens autres qu'un champ magnétique a eu un impact énorme sur la technologie. L'exemple le plus connu de ceci est le mécanisme de transfert de spin prédite par Slonczewski 1 et 2. par Berger dans lequel un transfert de courant électrique polarisé en spin moment cinétique à la ferromagnétique et commute son orientation. mémoires magnétiques à base de ce mécanisme (ST-MRAM) sont déjà disponibles dans le commerce, sont non-volatiles, ont une meilleure efficacité énergétique, et sont plus facilement évolutive à des dispositifs plus petits que la plupart des mémoires classiques 3. Un autre exemple est des matériaux magnéto-électriques (ou multiferroïques) 4 , 5, 6, dans lequel l'amplitude de l'aimantation peut être contrôlée par un champ électrique. Pour le fonctionnement de la température ambiante, les matériaux sont fabriqués par magnétoélectrique hétérostructures d'ingénierie combinant des matériaux ferroélectriques et ferromagnétiques qui sont couplés par la souche à leur interface. De tels matériaux pourraient également avoir des applications dans la mémoire à faible latence. Encore un autre mécanisme prometteur pour contrôler des propriétés ferromagnétiques comprend la commande de la température de transition de films minces ferromagnétiques en utilisant un champ électrique 7, 8, 9 -cette exploite la sensibilité des propriétés magnétiques à la densité de porteurs électroniques mis au point par l'effet de champ.
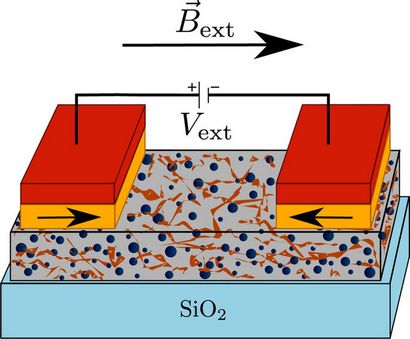
Figure 2: aimantation et de la capacité pour les différents processus d'initialisation.
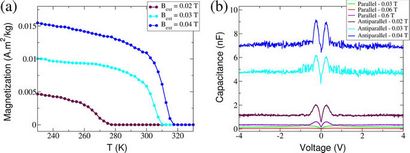
(A) de magnétisation en fonction de la température pour les échantillons initialisées avec différents Bext. La température de transition peut être amené à varier de 276 K (Bext = 0,02 T) à 317 K (Bext = 0,04 T). (B) Mesure de la capacité de plusieurs différents Bext correspondant à la configuration des électrodes distinctes (voir le texte et la Fig. 1 pour les détails).
Nous examinons d'abord les propriétés de transport électronique dépendant de la rotation du dispositif. On injecte un courant électrique sur le dispositif à travers les électrodes ferromagnétiques tandis qu'un champ magnétique externe est appliqué au système pour entraîner la configuration des électrodes. Nous avons mesuré la résistance électrique de l'appareil tout en faisant varier graduellement la puissance du champ magnétique. La figure 3 (a) montre le résultat d'une telle mesure.
Figure 3: propriétés électriques de l'appareil.
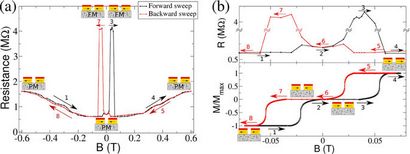
(A) la résistance électrique de l'appareil en fonction de la Bext. (B) ferromagnétique ancrée réponse des électrodes à un champ magnétique externe (en bas) et un haut-soufflage des données de résistance dans la même gamme de champ (en haut). Les mesures montrent deux sauts distincts dans la résistance, l'une correspondant à la magnétorésistance géante et l'autre en raison d'une transition ferromagnétique.
Pour comprendre cette transition ferromagnétique, nous estimons d'abord l'interaction magnétostatique directe entre les nanoparticules d'oxyde de fer. Nous constatons que cela est de plusieurs ordres de grandeur plus faible que kBTroom ce qui implique qu'il peut être exclu que l'origine du magnétisme dans ce système. Cela explique pourquoi le système reste toujours paramagnétique lorsque aucun courant est passé à travers elle. En outre, les états électroniques localisés sont nécessaires pour expliquer l'origine du ferromagnétisme, car aucun ferromagnétisme est observé dans des expériences sans l'oxyde de graphène partiellement réduit, par exemple, quand il est remplacé par la conduite très graphène ou fortement réduit l'oxyde de graphène.
La prochaine étape logique consiste à inclure un couplage en forme de Zeeman entre les électrons et les sauts de nanoparticules d'oxyde de fer. Cela donnera lieu à une interaction efficace entre les nanoparticules à médiation par la mer d'électrons à polarisation de spin de saut [sans spin-déséquilibre, cela est reminescent du bien connu Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction 12, 13, 14 ]. Fondamentalement, un électron au voisinage d'une nanoparticule conserve des informations sur l'orientation qui sera alors visible par les autres nanoparticules. Les estimations de l'ampleur de ce couplage se révèlent difficiles en raison des incertitudes de plusieurs paramètres du système. Cependant, les estimations raisonnables pour les paramètres matériels (voir informations supplémentaires) donnent à penser que l'échelle d'énergie de ces interactions médiation peut être de l'ordre de kBTroom. Ceci est donc l'explication la plus plausible pour les phénomènes observés. Dans ce qui suit, nous prenons à la J0 échelle du couplage entre l'électron et sautillante la nanoparticule. Ce sera une entrée dans les calculs théoriques.
Avec un tel mécanisme à l'esprit que nous pouvons écrire un hamiltonien microscopique efficace régissant un système de saut d'électrons de spin et des moments magnétiques localisés d'oxyde de fer. Nous utilisons des moments Ising pour le modèle et ne croyons pas que le comportement serait qualitativement différent pour une information supplémentaire de choix, voir différents. Le hamiltonien lit
où le () représente la partie régissant les électrons libres (moments iste), Il -e (HM -M) représente la partie contenant les interactions électron-électron (interactions dipôle-dipôle), alors qu'il -M représente la partie contenant le interaction Zeeman entre les sauts des électrons et des moments Ising. Dans ce qui suit, nous mettons de côté les termes et, sans rapport avec les calculs suivants, et, par souci de simplicité, ne pas tenir compte du terme Il -e. Dans l'esprit de RKKY 12, 13, 14 interaction, compte tenu des termes de H qui se rabattent le spin des électrons sauteuses, et en employant plusieurs simplifications au calcul (voir informations supplémentaires), on constate que l'intégration à des degrés de liberté des électrons hopping donne lieu à l'hamiltonien suivant pour les moments Ising (voir informations supplémentaires)
où Mα représente le moment magnétique indexé par α (exprimé en termes de Bohr magnétons, Mα = μBmαλα. avec λα = ± 1), rαβ représente le distance entre les deux moments magnétiques indexés par α et β. la constante K lit K ≡ J0μ0μBA. tandis que nσ est synonyme de la densité moyenne d'électrons de spin σ hopping = +, -. Le premier terme agit donc sur chaque instant Ising comme un champ magnétique effectif généré par le nuage de sauts d'électrons de spin-déséquilibrés. Le deuxième terme est un terme d'interaction d'échange indirect local entre les différents moments de Ising, avec le paramètre d'échange RKKY de type J (r. N +. N-) donnée par
où et est donnée par l'équation ci-dessus Dans les fonctions, et lues
où nous avons défini. Dans de ces expressions (μB) représente la permittivité du vide (Bohr de magnéton), m * pour la masse effective du gaz d'électrons de saut libre, tandis que A (B) représente l'amplitude d'un électron à l'état de spin σ avoir son spin inchangé (retourné) lors de l'interaction avec une nanoparticule.
A partir de la figure. 2 (b) nous estimons les densités électroniques moyenne de l'échantillon, n ±. constatent qu'ils sont généralement de petite taille tels que les interactions premiers voisins sont généralement ferromagnétique - voir des informations supplémentaires. En supposant que nous concluons que J (r. N +. N) est 4 (a) un minimum de spin déséquilibre nul, de plus en plus avec l'augmentation de voir spin-déséquilibre Fig.. Ceci est en contraste avec le résultat RKKY typique où aucun spin-flips des électrons sont considérés. Notre résultat d'analyse explique comment les augmentations de couplage ferromagnétique avec spin-déséquilibre expliquant l'observation expérimentale que l'aimantation disparaît sans spin déséquilibre et augmente avec spin-déséquilibre plus important.
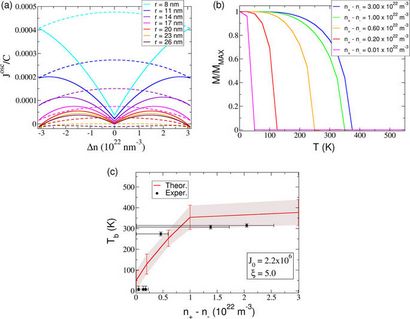
(A) Résumé de la partie oscillante du paramètre d'échange [voir l'équation (3)] pour plusieurs distances entre les nanoparticules. La constante C divisant J osc est le facteur principal dans l'équation (3). Nous traçons le cas où les deux sont autorisés spin-flips de pas électronique (courbes en pointillés) et le cas où ceux-ci sont autorisés (courbes pleines). (B) l'aimantation en fonction de la température pour différentes forces de couplage d'échange indirect. (C) Comparaison entre la température de blocage expérimentale et théorique en fonction de la force du spin-déséquilibre (les paramètres d'ajustement théoriques utilisés étaient J0 = 2,2 × 10 6 et ξ = 5 nm). Les résultats de Monte Carlo de panneaux (b) et (c) ont été obtenus pour les simulations (avec 79507 moments iste) à partir d'un état hautement ordonné (voir informations supplémentaires) qui utilisent l'algorithme Metropolis. Ils explorent la région de l'espace de phase à proximité du minimum mondial d'énergie, et indiquent que le système peut montrer ordre à longue distance si les grappes sont d'abord alignés par un champ magnétique externe.
trouble forte supprime de façon exponentielle la valeur typique de l'interaction RKKY 19, 20, 21, comme J (r. n +. n-) → J (r. n +. n-) e -r / ξ. où dans le boîtier métallique ξ est libre parcours moyen de l'électron. Étant donné que notre système est fortement ξ désordonnée devrait être faible, et la suppression exponentielle tue essentiellement des interactions plus, tous à distance tels que les seules interactions pertinentes dans notre système sont celles comparables avec celles du premier voisin. Par conséquent, toutes les interactions pertinentes sont ferromagnétiques. Pour comparer avec l'expérience que nous prenons ξ être un paramètre d'ajustement comparable à l'espacement entre les nanoparticules.
Les résultats expérimentaux suggèrent fortement que le terme du premier ordre dans l'équation (2) est sans importance par rapport au deuxième ordre une (voir l'information complémentaire). Ceci est parfaitement compatible avec le modèle théorique en dépit du fait que l'équation hamiltonien-voir efficace (2) -arises d'une extension de la série sur l'interaction électron-nanoparticule. L'amplitude relative de la première et de hamiltonienne effective termes de second ordre est déterminé par les paramètres extérieurs (n + -n-. Ξ. J0 m. *. A et B) plutôt que par le paramètre d'extension. Les paramètres utilisés pour obtenir les résultats de la Fig. 4. produisent un deuxième terme d'ordre d'au moins un ordre de grandeur supérieur au premier ordre un, pour la gamme de spin-déséquilibres estimés à partir des résultats expérimentaux. En conséquence, a été considéré que le second terme de l'ordre lors de l'exécution des simulations de Monte Carlo.
Afin d'étudier l'ordre magnétique du modèle d'Ising désordonné 3D résultant de l'intégration des degrés de liberté électroniques, nous avons effectué des simulations de Monte Carlo en utilisant notre propre implémentation de Metropolis algorithme spin-flip unique 22 et algorithme de groupe Wolf 23.