- Fonctions d'analyse interceptent Math
Trouver INTERCEPTIONS X et Y
Ligne :
Examinez le graphique de la ligne à gauche. Ce graphique manque beaucoup de choses. Il a besoin de flèches sur l'axe et sur les deux extrémités de la ligne. Le graphique manque également des étiquettes des axes x et y et, plus important encore, des étiquettes des axes d'intervalle. Mais, supposons que chaque case est un intervalle:
La ligne croise l'axe des x à (-1,0), de sorte -1 est l'abscisse à l'origine.
La ligne croise l'axe des y à (0,1), de sorte que 1 est l'ordonnée à l'origine.
y = x + 1
0 = x + 1
-1 = x donc, même si vous ne disposez pas d'un graphique, vous pouvez résoudre pour les interceptions (vous pouvez appliquer la même substitute- 0-technique pour trouver l'ordonnée à l'origine)
- les lignes auront pas plus d'un x à l'origine et pas plus d'une ordonnée à l'origine
# 65279; Parabole.
Examinez la parabole à droite. Juste en regardant le graphique, nous pouvons voir qu'il n'y aura pas de x à l'origine parce que le graphique ne sera jamais toucher l'axe des x (le sommet et le plus bas le graphique jamais atteindre est (1,1))
Le x-intercept est donc pas / NA (rappelez-vous que « 0 » est pas la même chose que « aucun » dans le monde des mathématiques).
L'ordonnée à l'origine est de 2 car le graphique touche de l'axe y à (0,2).
On peut voir les deux interceptions, ou leur absence, juste en regardant le graphique, mais on pourrait aussi remplacer 0 dans la variable x pour trouver notre ordonnée à l'origine. Cependant, nous ne pouvons pas le faire pour trouver notre x à l'origine. nous au lieu besoin d'utiliser la formule quadratique. Voir la vidéo ci-dessous pour l'aide à mémoriser la formule, et l'exemple ci-dessous pour plus parabola direction.
En huitième année, quand je commence à apprendre la fonction du second degré, mon professeur nous a fait regarder cette chanson à plusieurs reprises tous les jours, et nous avons dû se lever, chanter et applaudir. Il était un peu embarrassant et très ennuyeux à la fin, mais je n'ai pas oublié l'équation depuis, et mes amis et je marmonner encore la chanson que nous écrivons l'équation.
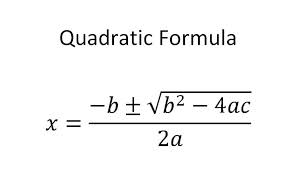
Nous pouvons voir que l'ordonnée à l'origine est -1.
Les abscisses à l'origine sont à -1 et 1.
Mais supposons que nous ne pouvions pas voir où les abscisses se sont produits. On peut toujours utiliser la formule quadratique:
x = (-b + SQRT (b) ²-4ac) / 2a
Pour utiliser cette formule, nous devons comprendre un peu plus sur la façon dont les formules sont créées parabola.
y = ax² + bx + c
Prenez la fonction à gauche, tous auront dans parábolas ce cas, un terme qui est carré, il est x². Nous n'avons pas un terme x, mais nous avons un changement vers le bas 1. Notre équation est y = x²-1. Ainsi, dans l'équation du second degré, notre a = 1, b = 0 notre et notre c = -1. Maintenant, nous devons brancher nos termes et résoudre:
x = (0 + SQRT (0) ²-4 (1) (- 1)) / 2 (1)
x = (+ SQRT 4) / 2
x = + 2/2
x = + 1
Nos x-INTERCEPTIONS sont positifs et négatifs 1 1.
Ainsi, en regardant le graphique ou en utilisant l'équation du second degré et la mise à 0. x nous pouvons trouver le X- et Y- INTERCEPTIONS. Bien qu'il travaille sur beaucoup plus de travail, dans les deux sens devrait vous donner la même réponse si vos calculs sont exacts, et les deux voies peuvent également être utilisés pour vérifier votre solution.
- parábolas n'a pas plus de deux X intercepte et pas plus d'une ordonnée à l'origine
équations valeur absolue ressemblent beaucoup à un parabola pointu. A gauche est le graphique de la valeur absolue des parents. Les intercepts et y- sont X- deux 0.
- CUM h comme une parabole, les équations de valeur absolue n'a pas plus de deux X intercepte et pas plus d'une interception y-
En jetant un regard sur la fonction à droite, on voit qu'il ya une ordonnée à l'origine et deux abscisses. L'ordonnée y- est 2, et les abscisses à l'origine sont à -4 et -2.
Si nous avons pu déterminer les intercepts en regardant le graphique, nous pouvons brancher 0 dans la variable que nous ne cherchons pas à trouver:
Trouver ordonnée à l'origine:
y = I0 + 3I-1
y = I3I-1
y = 2
Trouver x-INTERCEPTIONS:
0 = Ix + 3I-1
0 = x + 1/3 et 0 = x + 3 + 1
x = -2 et x = -4
Notez que nous avons traité le 1 comme + 1.
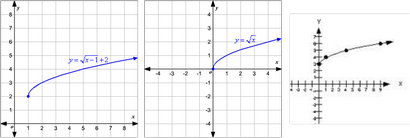
Tous les trois de ces équations de racine carrée sont des fonctions.
Racine carrée .T ici sont trois types d'équations de racine carrée, autant que x et y INTERCEPTIONS:
- 1 x à l'origine, une ordonnée à l'origine
- 1 x à l'origine, non ordonnée à l'origine / non abscisse à l'origine, une ordonnée à l'origine
- 0 abscisse à l'origine, 0 ordonnée à l'origine
- Regardez la première fonction de la racine carrée. L'équation ne sera jamais toucher l'axe des x ou l'axe y, de sorte que la fonction ne dispose pas d'un X- ou intercepter y-.
- Maintenant, regardez la deuxième fonction de la racine carrée. ceci a 1 x à l'origine et une ordonnée à l'origine, à la fois à (0,0). Par conséquent, les intercepts et y- sont X- 0.
- La troisième fonction racine carrée disposition ordonnée à l'origine et non abscisse à l'origine. L'ordonnée à l'origine est 3, mais nous pouvons voir que le graphique ne sera jamais toucher l'axe des x.
Trouvez l'ordonnée à l'origine:
y = SQRT (0) 3
y = 3
Trouver l'abscisse à:
0 = SQRT (x) + 3
-3 = SQRT (x)
T est ici pas x à l'origine parce que le graphique ne sera jamais toucher x = -3. L'ordonnée à l'origine est 3 et qui est la plage la plus basse que ce graphique jamais atteint. Nous pouvons confirmer cela en regardant le graphique et de voir que la fonction ne touche jamais l'axe x. Les graphiques sont une excellente façon de vérifier votre travail et gagner du temps.