La division Fractions Utilisation Soustraction répétée, Remise en cause Mon métacognition
Je parlais avec un groupe d'élèves de 5 ème aujourd'hui ...
Moi: Vous savez que l'année prochaine, vous devrez être en mesure de diviser une fraction par une fraction et non seulement une fraction d'un nombre entier? (MCC6.NS.1)
Étudiant: Je peux le faire en ce moment M. Fletch! Je ne ai pas besoin d'attendre l'année prochaine!
Moi: Ah oui? Comment c'est?
Étudiant: Eh bien toute division, se répète droit de soustraction?
Je suis retourné 5 minutes plus tard avec le problème suivant et a demandé aux étudiants de le résoudre en utilisant la soustraction répétée. Sam avait 1 ½ tasses de farine dans le placard. Il avait besoin 2/5 d'une tasse pour faire 1 lot de cookies. Combien de lots de cookies peut faire Sam?
Je ne l'ai pas résoudre le problème à l'avance et juste fouetté ensemble quelques chiffres (silly me). Après avoir travaillé exclusivement avec des modèles à ce point et ne jamais tenter moi-même soustraction répétée pour les fractions, je pensais que ce serait logique. Je crois comprendre que la soustraction répétée et la division se sont main dans la main, bien que ce n'est pas la méthode la plus efficace ... mais une précision. La solution de l'étudiant.

Tout était génial! Je me suis vite changé le nombre mélangé dans une fraction impropre, inversée puis multiplièrent. Oui, je sais que c'est super procédure mais je voulais vérifier rapidement la solution des étudiants (disclaimer: Je comprends pourquoi inverti - fonctionne multiplier alors je suis d'accord pour l'utiliser).
Me parle à moi-même: Et la réponse est ... 3 et 3/4. QU'EST-CE QUE LE. Comment c'est?
J'ai regardé à plusieurs reprises au travail de l'élève et double vérifié pour vous assurer qu'il avait fait aucune erreur. Tout fait sens qui m'a complètement dérouté et il était!
Me: Dessiner un modèle pour représenter ce que vous venez de faire.
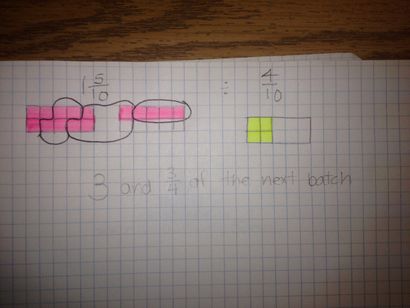
Étudiant: Mais j'ai 2 réponses différentes et je sais que mon dessin est juste.
Moi. Combien de dixièmes faire un lot et combien de dixièmes sont « restes »?
Étudiant: Eh bien je dois 4/10 et je n'ai 3/10 et (l'explosion-ampoule) ...... Je ..Oh obtenir! Il faut 4/10 d'une tasse pour faire un lot et 3/10 dans la soustraction répétée est 3/10 du 4/10 nécessaire. J'ai donc 3/4 du lot suivant. Donc, la réponse est vraiment 3 et 3/4 d'un lot!
Règle: si vous ne pouvez pas le sens de votre pensée à travers un modèle, vous ne comprenez probablement pas!