La prévision avec réglage saisonnier et linéaire lissage exponentiel
la mise en œuvre de la feuille de calcul de l'ajustement saisonnier et lissage exponentiel
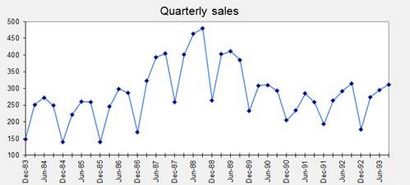
Pour obtenir une copie du fichier de feuille de calcul lui-même, cliquez ici. La version de lissage exponentiel linéaire qui sera utilisé ici à des fins de démonstration est la version de Brown, simplement parce qu'il peut être mis en œuvre avec une seule colonne de formules et il n'y a qu'un lissage constant d'optimiser. Habituellement, il est préférable d'utiliser la version de Holt qui a des constantes de lissage séparées pour le niveau et la tendance.
Le processus de prévision se déroule comme suit: (i) d'abord les données sont corrigées des variations saisonnières; (Ii) puis les prévisions sont générées pour les données corrigées des variations saisonnières par lissage exponentiel linéaire; et (iii) Enfin, les prévisions corrigées des variations saisonnières sont « reseasonalized » pour obtenir des prévisions pour la série originale. Le processus d'ajustement saisonnier est effectué dans les colonnes D à G.
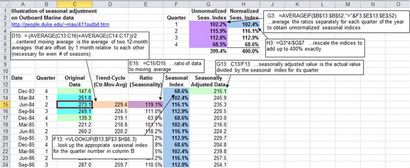
La première étape de réglage saisonnier consiste à calculer une moyenne (réalisée ici dans la colonne D) mobile centrée. Cela peut être fait en prenant la moyenne de deux d'un an à l'échelle des moyennes qui sont décalées d'une période par rapport à l'autre. (Une combinaison de deux moyennes de décalage au lieu d'une moyenne unique est nécessaire à des fins de centrage lorsque le nombre de périodes est pair.) L'étape suivante consiste à calculer le rapport de déplacement --i.e moyenne. les données d'origine divisé par la moyenne mobile dans chaque période - qui est effectuée ici dans la colonne E. (Ceci est également appelé la composante « tendance-cycle » du modèle, dans la mesure où les effets de tendance et du cycle économique pourraient être considérés comme tout ce qui reste après la moyenne sur la valeur d'une année de données. Bien sûr, les changements de mois en mois qui ne sont pas en raison de la saisonnalité pourraient être déterminés par de nombreux autres facteurs, mais la moyenne de 12 mois adoucit sur eux dans une grande mesure. ) L'indice saisonnier estimé pour chaque saison est calculée en premier la moyenne de tous les rapports pour cette saison particulière, qui se fait dans les cellules G3-G6 en utilisant une formule AVERAGEIF. Les ratios moyens sont alors redimensionnées pour que leur somme à exactement 100% fois le nombre de périodes dans une saison, ou 400% dans ce cas, ce qui se fait dans les cellules H3-H6. Ci-dessous dans la colonne F, les formules RECHERCHEV sont utilisées pour insérer la valeur d'index saisonnier approprié dans chaque ligne du tableau de données, selon le trimestre de l'année, il représente. La moyenne mobile centrée et les données corrigées des variations saisonnières finissent par ressembler à ceci:
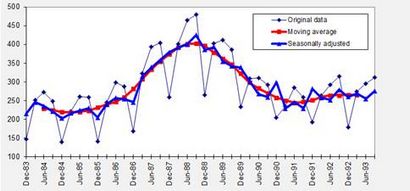
Notez que la moyenne mobile ressemble généralement à une version plus lisse de la série corrigée des variations saisonnières, et il est plus court sur les deux extrémités.
Une autre feuille de calcul dans le même fichier Excel montre l'application du modèle de lissage exponentiel linéaire aux données corrigées des variations saisonnières, à partir de la colonne G.
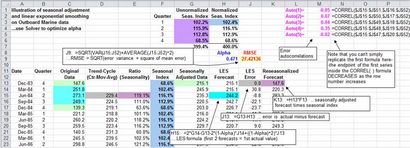
est entré une valeur pour la constante de lissage (alpha) au-dessus de la colonne de prévision (ici, dans la cellule H9) et pour des raisons pratiques, il se voit attribuer le nom de la plage « Alpha ». (Le nom est attribué à l'aide de la commande « Insertion / Nom / Créer ».) Le modèle LES est initialisé en définissant les deux premières prévisions correspondant à la première valeur réelle de la série corrigée des variations saisonnières. La formule utilisée ici pour les prévisions LES est la forme récursive simple équation du modèle de Brown:
Cette formule est entrée dans la cellule correspondant à la troisième période (ici, H15 cellulaire) et copié à partir de là. Notez que les prévisions LES pour la période en cours se réfère aux deux observations précédentes et les deux erreurs de prévision précédentes, ainsi que de la valeur de alpha. Ainsi, la formule de prévision à la ligne 15 se réfère uniquement à des données qui se trouvaient dans la rangée 14 et plus tôt. (Bien sûr, si l'on voulait utiliser simple, au lieu de lissage exponentiel linéaire, on pourrait substituer la formule SES ici à la place. On peut aussi utiliser plutôt que le modèle LES Brown Holt, qui nécessiterait deux colonnes de formules pour calculer le niveau et la tendance qui sont utilisés dans les prévisions.)
Les erreurs sont calculées dans la colonne suivante (ici, colonne J) en soustrayant les prévisions des valeurs réelles. La racine erreur quadratique moyenne est calculée comme la racine carrée de la variance des erreurs plus le carré de la moyenne. (Cela découle de l'identité mathématique: MSE = ÉCART (erreurs) + (moyenne (erreurs)) ^ 2.) Dans le calcul de la moyenne et la variance des erreurs dans cette formule, les deux premières périodes sont exclues parce que le modèle ne fait pas commencer la prévision jusqu'à ce que la troisième période (ligne 15 sur la feuille de calcul). La valeur optimale de l'alpha se trouve soit en modifiant manuellement alpha jusqu'à ce que le RMSE minimum se trouve, ou bien vous pouvez utiliser le « Solver » pour effectuer une minimisation exacte. La valeur alpha de ce que le Solver trouvé est représentée ici (alpha = 0,471).
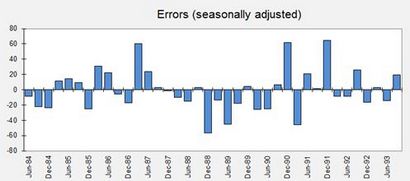
Il est généralement une bonne idée de tracer les erreurs du modèle (en unités transformées) et aussi pour calculer et tracer leurs autocorrélations à des retards jusqu'à une saison. Voici un terrain de séries chronologiques des erreurs (données désaisonnalisées):
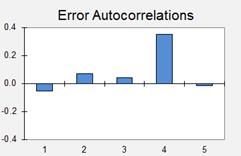
Les autocorrélations d'erreur sont calculées en utilisant la fonction pour calculer les corrélations des erreurs avec eux-mêmes décalage d'un ou plusieurs périodes CORREL () - les coordonnées figurent dans le modèle de feuille de calcul. Voici une représentation graphique des autocorrélations des erreurs au cours des cinq premiers retards:
Au bas de la feuille de calcul, la formule de prévision est « bootstrapped » dans l'avenir en substituant simplement les prévisions pour les valeurs réelles au point où les données réelles s'écoule - i.e.. où « l'avenir » commence. (En d'autres termes, dans chaque cellule où une valeur future des données se produirait, est insérée une référence de cellule qui pointe à la prévision faite pour cette période.) Toutes les autres formules sont simplement copiées vers le bas en haut:
Notez que les erreurs pour les prévisions de l'avenir sont tous calculés à zéro. Cela ne signifie pas que les erreurs réelles seront nuls, mais il reflète simplement le fait que, aux fins de prévision, nous partons du principe que les données futures égales aux prévisions en moyenne. Les prévisions pour les ERP résultant des données corrigées des variations saisonnières ressemblent à ceci:
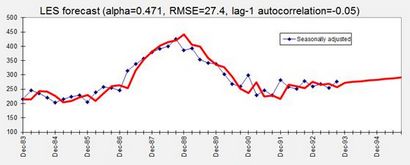
Avec cette valeur particulière de l'alpha, ce qui est optimal pour les prévisions d'une période à venir, la tendance projetée est légèrement à la hausse, ce qui reflète la tendance locale qui a été observée au cours des 2 dernières années. Pour les autres valeurs d'alpha, une projection de tendance très différente pourrait être obtenue. Il est généralement une bonne idée de voir ce qui se passe à la projection de tendance à long terme lorsque alpha est varié, parce que la valeur qui est le mieux pour les prévisions à court terme ne sera pas nécessairement la meilleure valeur pour prédire l'avenir plus lointain. Par exemple, voici le résultat qui est obtenu si la valeur de alpha est réglé à 0,25 manuellement:
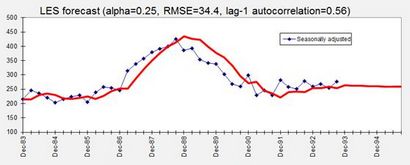
La tendance à long terme prévu est maintenant négatif plutôt que positif! Avec une valeur plus petite de l'alpha, le modèle met plus de poids sur des données plus anciennes dans son estimation du niveau actuel et tendance, et ses prévisions à long terme reflètent la tendance à la baisse observée au cours des 5 dernières années, plutôt que la tendance à la hausse plus récente. Ce tableau illustre aussi clairement comment le modèle avec une plus petite valeur de l'alpha est plus lente à répondre aux « points d'inflexion » dans les données et a donc tendance à faire une erreur du même signe pour plusieurs périodes consécutives. Ses erreurs de prévision 1 étape à venir sont plus grandes en moyenne que ceux obtenus avant (RMSE de 34,4 plutôt que 27,4) et fortement autocorrélées positivement. Le retard de 1 autocorrélation de 0,56 dépasse largement la valeur calculée ci-dessus de 0,33 pour une déviation statistiquement significative de zéro. Comme alternative à tourner la manivelle sur la valeur de l'alpha afin d'introduire plus de conservatisme dans les prévisions à long terme, un facteur « tendance amortissement » est parfois ajouté au modèle afin de rendre la tendance projetée aplatissent après quelques périodes.
La dernière étape dans la construction du modèle de prévision est aux prévisions LES « reasonalize » en les multipliant par les indices saisonniers appropriés. Ainsi, les prévisions reseasonalized dans la colonne I sont simplement le produit des indices saisonniers dans la colonne F et les prévisions LES corrigées des variations saisonnières dans la colonne H.
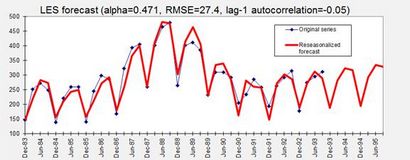
Les limites de confiance pour les prévisions plus d'une période à venir se creuseront généralement que l'horizon prévision augmente, en raison de l'incertitude sur le niveau et la tendance, ainsi que les facteurs saisonniers, mais il est difficile de les calculer en général par des méthodes analytiques. (La façon appropriée de calculer des limites de confiance pour les prévisions LES est en utilisant la théorie ARIMA, mais l'incertitude des indices saisonniers est une autre question.) Si vous voulez un intervalle de confiance réaliste pour une prévision plus d'une période à venir, en prenant toutes les sources de erreur en compte, votre meilleur pari est d'utiliser des méthodes empiriques: par exemple, pour obtenir un intervalle de confiance pour une prévision avant 2 étapes, vous pouvez créer une autre colonne sur la feuille de calcul pour calculer une prévision de 2 étape à l'avance pour chaque période ( par amorçage de la prévision d'une étape à l'avance). Puis calculer l'erreur quadratique moyenne des erreurs de prévision 2-étape avant et l'utiliser comme base pour un intervalle de confiance 2-étape avant.