Le graphique d'une fonction de radical (Algèbre 1, expressions Radical) - Mathplanet
Un radical comme vous souviendrez peut-être quelque chose qui est sous un signe radical par exemple une racine carrée. Une fonction contient un radical expression radical avec la variable indépendante (généralement x) dans le radicande. équations généralement radicales où le radical est une racine carrée est appelée fonctions racine carrée.
Un exemple d'une fonction de radical serait
Ceci est la fonction racine carrée mère et son graphique ressemble
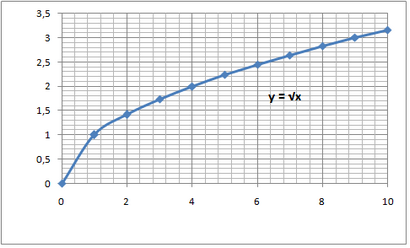
Si l'on compare cela à la fonction racine carrée
On remarquera que le graphe étire ou rétrécit verticalement lorsque nous varions une
$$ \ begin \ left | un \ right | > 0 \: \: \: \: \: \: \: - - \ Rightarrow vertical \: \\ 0 extensible<\left | a \right |<1 - - \Rightarrow vertical\: shrink\: \: \: \\ \end$$
Dans le graphique ci-dessous, nous avons des fonctions radicales avec des valeurs différentes d'un
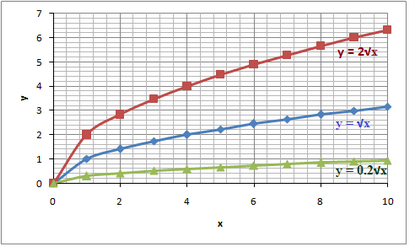
Si un < 0 the graph
Le reflet dans l'axe X du graphique
$$ y = \ left | a \ right | \ sqrt $$
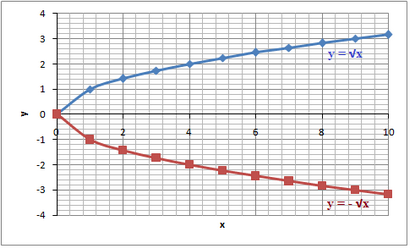
Une autre équation de racine carrée serait
Si vous regardez les graphiques ci-dessus qui ont tous c = 0, vous pouvez voir que tous ont une portée ≥ 0 (tous les graphiques commencent à x = 0 car il n'y a pas de véritables solutions à la racine carrée d'un nombre négatif). Si vous avez un c ≠ 0 vous aurez une fonction radicale qui commence dans (0, c). Un exemple de ceci peut être vu dans le graphique ci-dessous
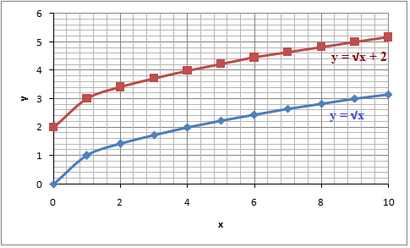
La valeur de b nous indique où le domaine de la fonction radicale commence. Encore une fois, si vous regardez la fonction parent, il a un b = 0 et commencer ainsi à (0, 0) Si vous avez un b ≠ 0 alors la fonction radicale commence en (b, 0).
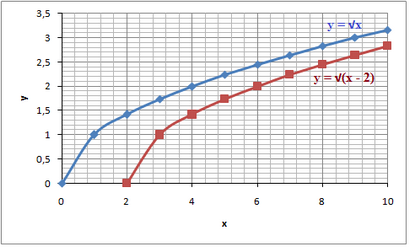
Si les deux b ≠ 0 et c ≠ 0, la fonction de radical commence en (b, c)
leçon de la vidéo
Comparez les fonctions radicales