Matematicas Visuales, développements d'avion des corps géométriques (3) Cylindres
Hilbert et Cohn-Vossen écrit sur le cylindre: « Le cylindre circulaire est la plus simple surface courbe Il peut être obtenu à partir des courbes les plus simples -la ligne droite et en déplaçant l'une dans les zones circulaires ligne droite autour du périmètrique d'un cercle tout en le gardant. perpendiculaire au plan du cercle. une autre façon d'obtenir le cylindre est en rotation d'une ligne droite autour d'un axe parallèle. Ainsi, le cylindre circulaire est une surface de révolution. les surfaces de révolution sont une classe importante de surfaces, caractérisé par la propriété qu'ils peuvent être générés par la rotation d'une courbe plane autour d'un axe situé dans le plan de la courbe « . (Hilber et Cohn-Vossen. La géométrie et l'imagination. Pag. 7).
Sur cette page, le cylindre est fermé par deux plans parallèles perpendiculaires à l'axe. Ces plans se coupent le cylindre en deux cercles. Nous appelons ces cercles les bases du cylindre.
L'intérêt principal de cette page est de voir comment un cylindre peut être développé dans un plan.


La surface latérale d'un cylindre est la surface d'un rectangle. La longueur de ce rectangle est le périmètrique de l'une des bases du cylindre. Nous pouvons calculer la surface latérale d'un cylindre:
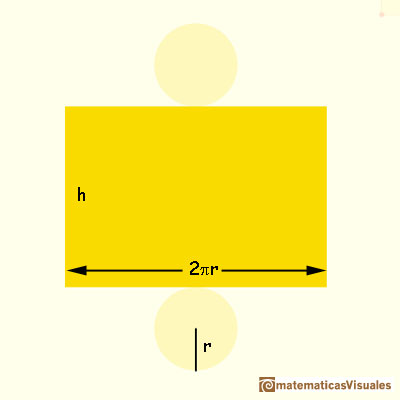
Pour calculer la superficie totale de la surface d'un cylindre, il faut ajouter la surface latérale ainsi que les cercles supérieurs et inférieurs (les deux cercles qui composent les extrémités du cylindre). Alors:
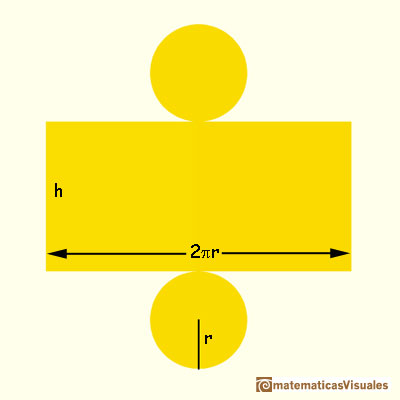
Vous souvenez-vous comment calculer le volume d'un cylindre?