Matrices concomitantes et à leurs applications en sciences de l'information ACA Extension au Web
Matrices concomitantes et à leurs applications en sciences de l'information: L'extension de l'ACA à l'environnement Web
Journal de la Société américaine pour la science et la technologie de l'information (JASIST)
matrices de co-occurrence, comme co-citation, co-mot, et les matrices co-liaison, ont été largement utilisés dans les sciences de l'information. Cependant, la confusion et la controverse ont entravé l'analyse statistique appropriée de ces données. Le problème sous-jacent, à notre avis, implique de comprendre la nature des différents types de matrices. Ce document traite de la différence entre une matrice de co-citations symétrique et une matrice de citation asymétrique ainsi que les techniques statistiques appropriées qui peuvent être appliqués à chacune de ces matrices, respectivement. mesures de similarité (comme le coefficient de corrélation de Pearson ou le cosinus) ne doivent pas être appliqués à la matrice de co-citations symétrique, mais peuvent être appliqués à la matrice de citation asymétrique pour dériver la matrice de proximité. L'argument est illustré par des exemples. L'étude étend ensuite l'application des matrices de co-occurrence à l'environnement Web où la nature des données disponibles et donc des méthodes de collecte de données sont différentes de celles des bases de données traditionnelles telles que la Science Citation Index. Un ensemble de données recueillies avec le moteur de recherche Google Scholar est analysé à l'aide des deux méthodes traditionnelles d'analyse à variables multiples et le nouveau logiciel de visualisation Pajek qui est basée sur l'analyse des réseaux sociaux et la théorie des graphes.
2. Symétrique Co-citation Matrice vs. Asymétrique Citation Matrice
2.1 La matrice de co-citations symétrique
Figure 1: matrice de co-citations (matrice symétrique)
2.2 La matrice de citation asymétrique
Une autre façon d'utiliser les données de citation est de construire une matrice sous la forme représentée à la figure 2. Nous allons montrer un exemple d'utilisation de cette matrice pour l'analyse co-citation auteur plus tard. Dans cette matrice, les lignes sont les journaux et les colonnes citant représentent des documents cités. Donc papier A est cité par du papier 1, 4 et 5, tandis que C est cité par le papier 2 et 3.
Figure 2: Matrice de citation (matrice asymétrique)
Figure 3: matrice de proximité dérivée des données sur la figure 2
Dans le cas de la matrice asymétrique (figure 2), les documents cités sont considérés comme des attributs des documents citant parce qu'ils sont contenus dans les listes de référence de celle-ci. Papier A part deux sur trois de ses documents citant D avec du papier de sorte que leur coefficient est un nombre compris entre 0 et 1, à savoir 0,295.
Tableau 1. kilométrages de vol entre 10 villes américaines
De toute évidence, cela est une matrice de proximité symétrique. Les mesures de données dissemblance. comme les grands nombres, les plus éloignés les villes sont, à savoir plus « dissemblables » ils sont dans un endroit. En entrant cette matrice dans SPSS et en choisissant PROXSCAL en option de MDS, on obtient la figure 3, qui est une application presque parfaite des positions relatives de ces villes (les positions sont relatives et la carte est inversée en termes de l'ouest et à l'est. Cependant, en raison de cette relativité des positions les résultats de MDS peuvent être mis en rotation librement pour l'interprétation).
Figure 4: Cartographie MDS (PROXSCAL) de dix villes américaines à l'aide de la matrice de distance initiale (normalisée contrainte brut = 0,0001)
Après l'application r de Pearson aux données du tableau 1, puis mapper cette nouvelle matrice avec MDS, on obtient une carte déformée des dix villes et le stress brut normalisée de cette image est très élevé (0,11341).
Figure 5: Cartographie MDS de dix villes américaines utilisant la matrice de corrélation de Pearson des distances (normalisée contrainte brut = 0,11341)
Apparemment, la figure 5 ne s'améliore pas sur la figure 4 (le stress est devenu très élevé). En utilisant les corrélations de Pearson au lieu des distances, la représentation est déformée. Par exemple, Los Angeles est positionné plus près de Seattle que San Francisco tandis que New York est plus proche de Chicago que de Washington, DC La corrélation de Pearson normalise les données en référence à la moyenne, et le modèle de co-occurrences comme variables, comme l'indique la corrélation de Pearson, est dans certains cas, différents des proximités du réseau.
3. similarité par rapport à des mesures de dissimilitude
Dans les premières versions de SPSS, seule l'option ALSCAL était disponible (la mesure de dissemblance seulement). Dans ce cas, une matrice de co-citation doit être convertie en une matrice de dissemblance avant qu'il ne soit entrée dans SPSS. Kruskal - Wish (. 1978, p 77) indiquent clairement que « Si les proximités des similitudes, ils doivent être « renversées » dans dissemblances, par exemple en formant dissemblance = (constante - similitude) où est judicieusement la valeur de la constante choisi « Si la mesure de similarité est compris entre 0 et 1 (par exemple, l'exemple ci-dessus en utilisant le r de Pearson pour obtenir la matrice de proximité de la figure 3), la constante peut être de 1, à savoir dissemblance =. (1 - similitude). L'un d'entre nous a mené des tests approfondis des formules et a constaté que les résultats de la cartographie de l'utilisation des mesures de dissimilitude après la conversion correcte de ressemblance avec dissemblance, et d'utiliser les mesures de similarité directement, sont toujours les mêmes.
4. Un exemple de co-auteur Analyse des citations (ACA)
4.1 Statistiques descriptives
Sur les (469 + 494 =) 963 documents ainsi récupérés, 902 contiennent 21,813 références. 279 dossiers contiennent au moins un co-citation à deux ou plusieurs auteurs de la liste des 24 auteurs à l'étude.
Il n'y a pas de documents citant contenant une référence à un seul auteur dans cet ensemble de 279 documents citant. Ainsi, cela peut avec raison être considéré comme un ensemble d'auteurs très co-citées. La figure 6 montre que l'on cite le papier même co-cité dix des auteurs inclus dans l'analyse.
Figure 6: Répartition des 279 cocitations en termes de nombre de co-auteurs cités dans un seul document citant
La figure 7 présente les citations totales de ces auteurs dans l'ensemble des documents citant. Notez que les scientométrie auteurs ont en moyenne un taux de citation de 44,6 (± 14,8), alors que les chercheurs recherche d'information ont une moyenne inférieure de 26,1 (± 6,5). Les taux de citation sont spécifiques sur le terrain, en effet.
Figure 7. Nombre de fois chacun des 24 auteurs est cité dans les 279 documents citant
Passons maintenant à partir de ces statistiques descriptives à une analyse des données.
4.2 Analyse des données de la matrice asymétrique
Tableau 2 corrélations de Pearson entre les 24 auteurs cités sur la base de 279 documents citant
La figure 8 montre les résultats de la saisie de la matrice asymétrique en PROXSCAL pour le MDS. La visualisation suggère que les chercheurs recherche d'information sont plus organisés le long d'un axe unique (presque horizontale) que les scientometricians le long d'une verticale. L'analyse des facteurs de la matrice confirme cette observation et permet d'informer cette image avec une interprétation quantitative.
PROXSCAL MDS sur la base de la matrice asymétrique (normalisée de contrainte brut = 0,044)
Composant pivotées matrice (A)
Méthode d'extraction: analyse en composantes principales. Méthode de rotation: Varimax avec normalisation Kaiser.
une rotation convergé en 7 itérations.
Tableau 3. L'analyse factorielle de la matrice asymétrique des 24 auteurs co-cités (N = 279).
Le produit d'analyse des facteurs (par définition) à partir de la matrice de corrélation de Pearson en tant que première étape dans le calcul de ces statistiques. Si nous entrons dans la matrice de corrélation de Pearson fournie dans le tableau 2 comme une matrice de similarité dans PROXSCAL on obtient la figure 9.
Figure 9:
PROXSCAL MDS sur la base de la matrice de corrélation de Pearson fournies dans le tableau 2 (normalisé du stress brut = 0,148).
Bien que cette image nous permet de faire la même observation qu'il ya deux groupes dans ces données (les scientifiques de recherche d'information sur le côté gauche et les scientometricians sur le côté droit), l'image est moins informative que le précédent et le stress est aggravé considérablement. La matrice de corrélation de Pearson contient moins d'informations que la matrice d'attributs d'origine en raison de l'hypothèse de normalité dans la distribution sous-jacente de ses statistiques. Étant donné que nos données ne sont pas normalement distribuées, on obtient une image déformée lorsque nous les entrée des données normalisées dans MDS. [3]
En faisant tourner la matrice, l'analyse factorielle nous permet de récupérer la structure sous-jacente en dépit des hypothèses sur la normalité de la distribution (Kim - Mueller, 1978).
De plus, l'analyse des facteurs nous permet de dessiner un diagramme de dispersion après optimisation des corrélations de Pearson en se référant aux vecteurs propres de la matrice. La représentation en trois dimensions correspondant illustre la division majeure entre les deux groupes et les structures fines au sein de chacun d'eux.
Terrain de facteur de la matrice asymétrique en rotation dans l'espace au moyen de trois facteurs (Varimax rotation; normalisation Kaiser).
4.3 Matrice Co-citation
Figure 11. PROXSCAL sur les données de co-citations (utilisé en tant que données ordinal, le stress = 0,04).
Lorsque nous appliquons cette même technique à la matrice de corrélation de Pearson basée sur la co-citation en entrée, comme est pratique courante dans ACA-on obtient Figure 12:
PROXSCAL sur la matrice de corrélation de Pearson à partir de données de co-citations (stress = 0,148).
4.4. Analyse des réseaux sociaux
Cette définition différente ne fait pas de différence pour la mise en correspondance parce que les algorithmes de visualisation dans Pajek-un programme qui a plus ou moins devenir la norme pour le réseau visualisation réduit toutes les valeurs d'abord aux valeurs binaires (uns et de zéros) et ne permet par la suite l'utilisateur de visualiser les valeurs en utilisant des tailles de ligne variables. [6] La figure 13 montre une visualisation de notre matrice de co-occurrence en utilisant Pajek et l'algorithme basé ressort de Kamada - Kawai (1989). Cet algorithme réduit le stress dans la représentation en termes de chercher à minimiser la teneur en énergie du système de ressort. Il peut être considéré comme équivalent à l'échelle multidimensionnelle non métrique.
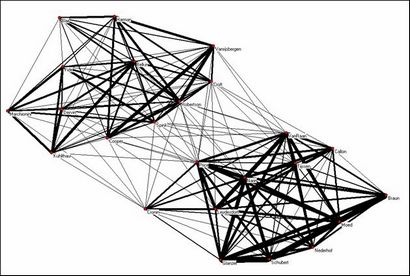
Figure 13: matrice Cooccurrence utilisant Pajek pour la visualisation
5. L'extension de l'ACA à la recherche sur Internet
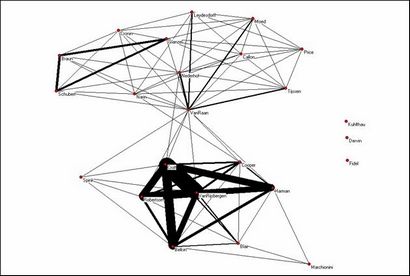
matrice de co-occurrence en utilisant Pajek pour la visualisation.
Bien que les deux groupes sont encore très visibles dans cette représentation, Van Raan obtient la position d'une plaque tournante reliant les deux sous-réseaux. Certains des scientifiques de récupération d'information ne disposent pas d'une visibilité sur le Web, mais quelques-uns des autres sont reliées plus étroitement que les scientometricians. Au sein du groupe scientométrie, on peut voir le dessin Van Raan principalement sur un groupe néerlandais, alors que le groupe « hongrois » présente également une relativement forte connexité.
terrain à trois facteurs de fichier cooccurrence basé sur les recherches Google Scholar
Ces interprétations peuvent encore être informés par l'analyse des facteurs. La figure 15 illustre les résultats. Un premier facteur (expliquant que 11,25% de la variance dans cette matrice) est dirigée à nouveau par Croft et Van Rijsbergen. Cet ensemble, cependant, comprend également un sous-ensemble des scientometricians. Le deuxième facteur (8,37%) peut être considérée comme un facteur a « Leiden », tandis que le troisième facteur (6,47%) peut être distingué en tant que groupe de scientometricians avec un (ancien) adresse Budapest. Ce modèle est un peu différent du motif représenté sur la figure 10, qui était basée sur les données de citation ISI, car la composante institutionnelle est renforcée dans la figure 15.
6. Conclusions et discussion
matrices de co-occurrence, comme co-citation, co-mot, et les matrices co-liaison, ont été largement utilisés dans la recherche en sciences de l'information. Cependant, la confusion et la controverse concernant l'analyse persiste statistique appropriée à appliquer. Un problème de racine est dans la compréhension de la nature des différents types de matrices. Cette étude a examiné les différences entre la matrice de co-citations symétrique et la matrice de citation asymétrique ainsi que les techniques statistiques appropriées qui peuvent être appliqués à ces matrices. Elle conclut que le coefficient de corrélation de Pearson ne doit pas être appliqué à une matrice de co-citations symétrique, mais peut être appliquée à la matrice de citation asymétrique afin de dériver la matrice de proximité qui est nécessaire pour une analyse telle que mise à l'échelle multidimensionnelle. Le document a également fait une distinction claire entre les matrices de similarité et dissemblance, et nous a montré comment elles doivent être définies lors de l'utilisation des logiciels statistiques tels que SPSS. Des exemples ont été utilisés pour soutenir nos arguments analytiques.
L'étude a étendu l'application des matrices de co-occurrence à l'environnement Web où la nature des données disponibles et donc des méthodes de collecte de données sont différentes de celles des bases de données traditionnelles, telles que celles de l'ISI. Un ensemble de données recueillies à l'aide du moteur de recherche Google Scholar a été analysé à l'aide à la fois l'analyse des facteurs traditionnels et le nouveau logiciel de visualisation Pajek qui est basée sur l'analyse des réseaux sociaux. Les limites de Pajek dans l'analyse des matrices de co-occurrence ont été signalées. Le seul but de cet article est de clarifier les questions entourant la nature et l'application des matrices de co-occurrence et de contribuer ainsi au développement de ce domaine de la science de l'information.
Burt, R. S. (1982). Vers une théorie structurale d'action. New York, etc. Academic Press.
Davison, M. L. (1983). mise à l'échelle pluridimensionnelle. New York: John Wiley.
Garfield, E. (1979). Citation indexation: la théorie et l'application de la science, la technologie et sciences humaines. New York: John Wiley.
Jones, W. P. - Furnas, G. W. (1987). Photos de pertinence: une analyse géométrique des mesures de similarité. Journal de l'American Society for Information Science, 36 (6), 420-442.
Kamada, T. - Kawai, S. (1989). Un algorithme pour dessiner un graphe non orienté général. Information Processing Letters, 31 (1), 7-15.
Kim, J.-O. - Mueller, C. W. (1978). Analyse factorielle, Méthodes statistiques et questions pratiques. Beverly Hills, etc. Sage.
Kruskal, J. B. - Wish, M. (1978). Mise à l'échelle pluridimensionnelle. Beverly Hills, etc. Sage.
Leydesdorff, L. (1987). Diverses méthodes pour la cartographie des sciences. Scientometrics 11, 291-320.
Leydesdorff, L. (1989). Les mots et les co-mots comme indicateurs de l'organisation intellectuelle. Politique de recherche, 18 (4), 209-223.
Schiffman, S. S. Reynolds, M. L. - Young, F. W. (1981). Introduction à la mise à l'échelle multidimensionnelle: la théorie, les méthodes et les applications. New York / Londres: Academic Press.
Siegel, S. - Castellan, N. J. Jr. 1988. Les statistiques non paramétriques pour les sciences du comportement. New York: McGraw-Hill.
Petit, H. - Sweeney, E. (1985). Clustering Science Citation Index Utilisation de cocitations I. Comparaison des méthodes. Scientometrics 7, 391-409
Blanc, H. D. - Griffith, B. (1981). Auteur cocitation: Une mesaure de la littérature des structures intellectuelles. Journal de l'American Society for Information Science. 32 (3), 163-171.