Sculpture symbolique et anneaux Borromées
Les anneaux Borromées peut être vu dans l'image suivante.
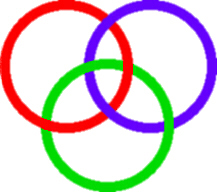
Comme vous pouvez le voir, il se compose de trois cercles, liés de sorte qu'ils ne peuvent pas être séparés. Mais aucun lien de cercle individuels avec une autre, il est seulement la figure dans son ensemble qui ne peut être démêlé.
Si vous essayez de faire les anneaux Borromées sur le fil, vous constaterez que vous ne pouvez pas faire des cercles réels à plat dans la figure. Il doit toujours être Kinks.
Le Maple image ci-dessous est un très bon exemple de ces petits défauts; il a été créé par I.J.Mcgee. en entrant le code en dessous.
L'image est produite en utilisant un tracé de tube à Maple, qui est elle suit la ligne d'une courbe, en créant un tube de section transversale circulaire. Il a dû prendre un certain temps pour obtenir le bon paramétrisation!
Il y a une autre preuve (lien externe) que les cercles Borromées plats n'existent pas, en utilisant la géométrie hyperbolique en quatre dimensions.
Il est cependant possible de produire avec des ellipses.
Il existe de nombreux exemples dans pas Knot (hors lien).
John Robinson a constaté que si vous utilisez des carrés au lieu de cercles que vous pouvez alors faire une figure réelle. Essayez vous-même avec des découpes en carton.
Il est également surprenant que la forme soulevée dans une forme extraordinaire, comme indiqué dans la création. Vous serez intéressés de constater que si elles sont correctement la forme est faite de la carte, alors il se plie aussi à plat. Ainsi, vous pouvez vous faire une sculpture de voyage!
Si vous aimez la géométrie et la trigonométrie, vous pouvez essayer de calculer les différentes distances entre les coins et les angles entre les parties. Des solutions efficaces pourraient être annoncés ici!
John expérimenta ensuite avec d'autres formes, et les résultats ont été GENESIS. et Intuition. Ses expériences en tant que sculpteur et ont inspiré vrai geometer mathématiciens d'explorer ces formes.
D'autres intéressants Liens externes
THEMES MATHÉMATIQUES
- Leuröbius Band - ce que l'on ressemble, les expériences d'essayer, et une belle rotation d'or qui vous permet de voir ce que l'on ressemble vraiment en 3D (facultatif comme 90Kb).
- Bernard Morin et le modèle Brehm - comment Bernard Morin a montré John Robinson le modèle Brehm du Möbius Band et comment faire un!
- Le plan projectif - comment créer et comprendre le plan projectif quand il est impossible de construire physiquement (ce qui a trait au modèle Brehm dans le plan projectif). En outre, la chaîne Trick Dirac.
- Faisceaux de fibres - ce qu'ils sont, comment les faire, et des exemples d'entre eux dans le travail de John Robinson.
- Nœuds et liens - Introduction au sujet de la théorie Knot, comprend l'histoire du sujet, et une rotation Immortalité mathématiquement construit (la minette étant l'un des nœuds les plus élémentaires).
- Torus Nœuds - deux pages expliquant les notions de base sur les nœuds tores avec l'aide d'excellents graphismes colorés. Il y a aussi des images en mouvement 3D des sculptures de John Robinson du nœud gordien et le rythme de la vie.
- Fractales 3 pages, l'introduction Fractales, compte tenu de l'itération, le joint Sierpinski et les applications du sujet.