Avant calcul polynomiale Division
Si vous éprouvez des difficultés à ce sujet, vous êtes au bon endroit. Si vous ne savez pas ce que cela est, et vous êtes curieux, c'est aussi le bon endroit pour vous! division polynomiale est assez importante, et est utilisé dans le calcul.
Quelle est la division polynomiale?
division polynomiale est quand on divise un polynôme par un autre. Un polynôme signifie simplement une expression où il y a plusieurs puissances de x. Voici quelques exemples qui nécessitent division polynomiale.
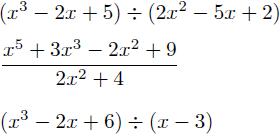
longue division est vraiment important de savoir, car il peut être utilisé pour diviser les deux polynômes. Il n'y a pas d'exceptions ou des règles à ce sujet. division synthétique est une belle astuce pour savoir, mais il est seulement pour un seul type de division polynomiale. la longue division les couvre tous. Permettez-moi de un problème pour vous montrer la technique de division. Je vais vous expliquer tout cela, étape par étape. Pour une raison quelconque, vous voulez faire la division dans cette expression:
Ceci est le format correct qui doit être utilisé lorsque vous faites division. Alors, quelle est la première étape? Nous devons examiner le diviseur, la chose en dehors de la boîte, sur le côté droit. Dans ce cas, x - 2. Dans le diviseur, vous ne regardez que la plus grande puissance de x. Dans cet exemple, nous avons seulement une x. Le coefficient est juste 1. Alors, nous regardons les x. Qu'est-ce que les temps x » est égal au premier terme du dividende? En d'autres termes, ce que x fois X³ est égal? Ceci est assez simple, et la réponse est évidemment x². Ceci est le premier terme du quotient (notre réponse). Ecrire ce sur le dessus de la ligne, exactement au-dessus du premier terme du dividende.
Maintenant, comme dans la division normale longue, on multiplie cette première partie de notre réponse par le diviseur, l'expression sur le côté droit. , Vous soustrayez alors que du dividende! Après cette soustraction, vous faire tomber le prochain terme du dividende, et répétez le processus. Je sais que cela semble compliqué quand vous lisez pour la première fois, mais je vais vous montrer ce que je veux dire.
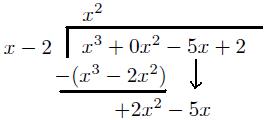
Voyez comme je l'ai fait? Maintenant, on répète le processus jusqu'à ce que le premier terme du diviseur ne peut plus « aller dans » le terme que nous regardons du dividende. Après cela, je vais vous expliquer ce que nous faisons. Pour l'instant, regardez le premier terme du diviseur, x. De cette nouvelle expression, 2x² - 5x, regardez le premier terme. Qu'est-ce que les temps x est égal à 2x²? Ensuite, nous continuons simplement faire ce que nous venons de faire. Je vais terminer le reste du processus.
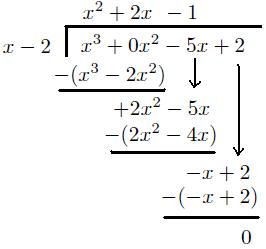
La réponse finale peut être écrit comme ça.
Je vais faire un exemple pour vous.

Voilà! Cette technique peut être utilisée pour diviser les deux polynômes. Essayez, comme il peut être utile dans plusieurs situations dans le calcul!
Bien. Vous maîtrisez la division longtemps maintenant, non? Vous avez cette baisse? Maintenant, vous voulez un truc? Est-ce que je suis censé faire maintenant? Bon, eh bien je pour vous. Ceci est appelé division synthétique. Maintenant, il ne fonctionne que dans une situation particulière, mais il peut être extrêmement utile parfois. Si vous ne me croyez pas, consultez ce post où j'avais besoin pour résoudre le problème. Je donne en fait l'explication complète de la division synthétique dans ce poste, mais je le ferai encore ici juste pour vous les gars peuvent le voir avec division. Le poste a été une question posée par un lecteur, poser des questions sur la façon de prendre la limite de quelque chose d'assez difficile. Cliquez ici pour aller droit au poste et voir comment je division synthétique.
Alors, quand peut-on utiliser la division synthétique? Une condition doit être remplie pour l'utiliser. Nous devons examiner le diviseur. Ceci est l'expression que nous divisons par. Cela doit être un seul x plus ou moins un nombre constant. Cela pourrait être x - 3, ou il pourrait être x + 10. Peu importe si elle est plus ou si elle est moins. Il a juste besoin d'être l'une de ces formes simples. Permettez-moi de vous montrer comment il est fait par un exemple.
Maintenant, il y a quelques similitudes avec la longue division. Tout d'abord, vous devez utiliser des supports de place de la même manière. Si vous n'avez pas un terme x² comme dans l'exemple ci-dessus, vous devez mettre un 0. En outre, le dernier numéro sur le fond est le reste, et est traité de la même manière que dans la longue division. Le reste sur le diviseur est ajouté à la solution, afin qu'il soit correct. Si le reste est égal à zéro, vous pouvez ignorer cette étape. D'accord, donc ci-dessous, je vais vous montrer la voie de mettre en place la division synthétique. Tout d'abord, vous devez penser du diviseur, x - 3, toujours dans ce pour. x - a. un peut être quelque chose, même un nombre négatif. Si le diviseur était x + 5, un serait -5, non? Placez -3, l'un, dans le coin supérieur droit. Puis, dans une ligne droite, à droite les coefficients de chaque terme. S'il est égal à zéro d'un terme, assurez-vous d'écrire 0. est inférieure à la façon de mettre en place la division. Laisser la place à une deuxième rangée sous la première, et tracer une ligne en vertu de cet espace.
Pour commencer, baissez le premier terme dans la rangée supérieure vers le bas.
Ensuite, multiplier le nombre dans le coin supérieur droit de ce numéro que vous venez de soulever directement vers le bas. Dans cet exemple, multiplier le 3 par l'1. Notez ce numéro dans la deuxième rangée sous le numéro suivant de la première rangée.
Ajoutez les deux chiffres qui sont maintenant juste au-dessus / dessous de l'autre, et d'écrire ce nombre en dessous.
Maintenant, répétez le processus. Multiplier le nombre supérieur droit par ce nouveau numéro inférieur. Ajoutez à cela le numéro suivant de la rangée supérieure. Et répéter jusqu'à ce qu'il n'y a plus de chiffres dans la rangée supérieure. Le nombre final dans la rangée du bas est le reste. Placez ce dans une boîte, et le laisser sur le côté où il appartient.
Non compris le reste, ce sont vos nouveaux coefficients! Le nouveau polynôme a la plus grande puissance de x qui est un de moins que la plus grande puissance qui était du dividende. Dans ce problème, la plus grande puissance de x original était X³, de sorte que la nouvelle puissance la plus élevée sera X². Il suffit de placer sur les coefficients, et ajouter le reste si nécessaire. C'est la solution!
Je crois que je l'ai expliqué mieux dans la solution que j'ai posté à la question d'un lecteur. Je vous invite à consulter cette page si vous avez encore des questions. Cliquez ici si vous souhaitez voir ce poste. Je vais vous montrer un exemple.
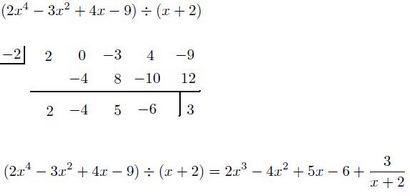
Est-ce que vous aimez les mathématiques et que vous voulez aider les autres? Il existe des programmes de certificat d'enseignement en ligne disponibles pour les futurs professeurs de mathématiques.