Calcul Vector Comprendre le produit Cross - BetterExplained
Le produit croisé accumule les interactions entre les différentes dimensions. Prendre deux vecteurs, nous pouvons écrire toutes les combinaisons de composants dans une grille:
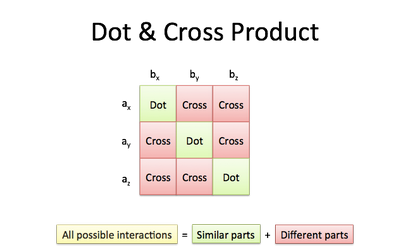
Cette grille complétée est le produit extérieur. qui peut être séparé dans l':
Produit scalaire. les interactions entre les dimensions similaires (x * x y * y. z * z)
Produit croisé. les interactions entre les différentes dimensions (x * y. y * z. z * x. etc.)
Le produit scalaire (VEC (a) · VEC (b)) mesure la similarité car il accumule les interactions que dans les dimensions correspondantes. Le calcul est simple avec 3 composants.
Le produit croisé (VEC écrit (a) fois VEC (b)) doit mesurer une demi-douzaine de « interactions croisées ». Le calcul semble complexe, mais le concept est simple: accumuler 6 différences individuelles pour le total.
Au lieu de penser « Quand ai-je besoin du produit croix? » Penser « Quand ai-je besoin d'interactions entre les différentes dimensions? ».
Zone, par exemple, est formé par des vecteurs pointant dans des directions différentes (plus orthogonale, mieux). En effet, le produit croisé mesure la zone couverte par deux vecteurs 3D (source):
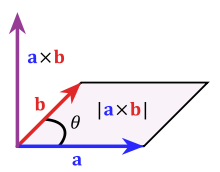
(Le « produit vectoriel » suppose vecteurs 3d, mais le concept étend à des dimensions supérieures).
Est-ce que l'intuition clé cliquez? Nous allons sauter dans les détails.
Définir le produit Cross
Le produit scalaire représente similitude vectoriel avec un seul numéro:
(Rappelez-vous que les fonctions trigonométriques sont des pourcentages.) Si le produit croisé (différence entre les vecteurs d'interaction) est un numéro unique aussi?
Essayons. Sine est la différence de pourcentage, afin que nous puissions utiliser:
Malheureusement, nous manque beaucoup de détails. x est égal à 100% à la fois différent de y et z. mais ne devrait pas y x * et x * z être différent de l'autre? Comme Tolstoï écrit: « Toutes les familles heureuses se ressemblent; chaque famille malheureuse est malheureuse à sa façon « .
Au lieu de cela, nous allons exprimer ces différences uniques comme un vecteur:
La taille du produit vectoriel est la « quantité de différence » numérique (avec sin (thêta) en pourcentage)
La direction du produit vectoriel est basé sur les deux entrées: il est la direction orthogonale à la fois (par exemple en favorisant ni)
Un résultat de vecteur représente le x * x * y et z séparément, bien que y et z sont tous les deux « 100% différent » de x.
(Si le produit scalaire être transformé en un vecteur aussi? Eh bien, nous avons les entrées et un pourcentage de similarité. Il n'y a pas nouvelle direction qui ne sont pas disponibles à partir de l'une des entrées.)
interprétation géométrique
Deux vecteurs déterminent un plan, et les points de produit croisé dans une direction différente à la fois (source):
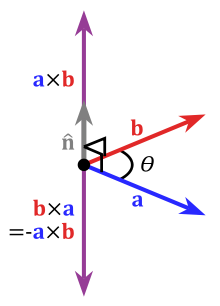
Voici le problème: il y a deux directions perpendiculaires. Par convention, on suppose un « système droitier » (source):
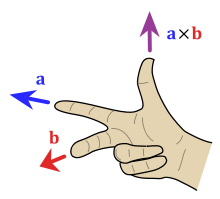
Si vous maintenez vos deux premiers doigts comme le montre le diagramme, le pouce pointe dans la direction du produit croix. Je me assure que l'orientation est correcte en balayant mon premier doigt de VEC (a) à VEC (b). Avec la direction compris, l'ampleur du produit croix est | a | | B | sin (thêta). qui est proportionnelle à l'amplitude de chaque vecteur et le « pourcentage de différence » (sinusoïdale).
La Croix Produit Pour Orthogonal vecteurs
Pour se rappeler la bonne règle de la main, écrire l'ordre xyz deux fois: xyzxyz. , Trouver suivant le modèle que vous recherchez:
- xy => z (x croix y est z)
- yz => x (y z transversale est x, on boucle autour de: y à z à x)
- zx => y
Donc, sans une formule, vous devriez être en mesure de calculer:
Encore une fois, ceci est parce que x croix y est positif z dans un système de coordonnées à droite. J'ai utilisé des vecteurs unitaires, mais nous pourrions échelle les termes:
Calcul de la Croix-produit
Lorsque les vecteurs sont croisés, chaque paire de composantes orthogonales (comme A_X fois b_y) jette un vote pour lequel le vecteur orthogonal doit pointer. 6 composantes, 6 voix, et leur total est le produit vectoriel. (Similaire au gradient. Où chaque axe jette un vote pour la direction de la plus grande augmentation.)
- xy => z et yx => -z (supposons vec (a) est d'abord, de sorte que xy signifie A_X b_y)
- yz => x et zy => -x
- zx => y et xz => -y
xy et yx combattre dans la direction z. Si ces termes sont égaux, comme dans (2, 1, 0) fois (2, 1, 1). il n'y a pas de composant de produit en croix dans la direction z (2 - 2 = 0).
La combinaison finale est:
où VEC (n) est le vecteur unitaire normal à vec (a) et vec (b).
Ne vous laissez pas effrayer:
- Il y a 6 termes, 3 positifs et négatifs 3
- Deux dimensions vote le troisième (si le terme z ne doit avoir des composantes y et x)
- L'ordre positif / négatif sont basées sur le motif de xyzxyz
Si vous aimez, il y a une preuve algébrique. que la formule est à la fois orthogonale et de la taille | a | | B | sin (thêta). mais j'aime l'intuition « de vote proportionnel ».
exemple Temps
Encore une fois, nous devons faire des produits simples croix dans notre tête:
Pourquoi? Nous avons traversé les axes x et y, nous donnant z (ou VEC (i) fois vec (j) = vec (k). En utilisant ces vecteurs unitaires). En traversant l'autre sens donne -vec (k).
Voici comment je marche à travers des exemples plus complexes:
- Faisons le dernier terme, la composante z. C'est (1) (5) moins (4) (2), ou 5 - 8 = -3. Je l'ai fait z d'abord parce qu'elle utilise x et y. les deux premiers termes. Essayez de voir (1) (5) comme « avant » que vous numérisez à partir du premier vecteur au second, et (4) (2) en arrière que vous passez du second vecteur au premier.
- Maintenant, la composante y: (3) (4) - (6) (1) = 12 - 6 = 6
- Maintenant, la composante x: (2) (6) - (5) (3) = 12 - 15 = -3
Ainsi, le total est (-3, 6, -3) que nous pouvons vérifier avec Wolfram Alpha.
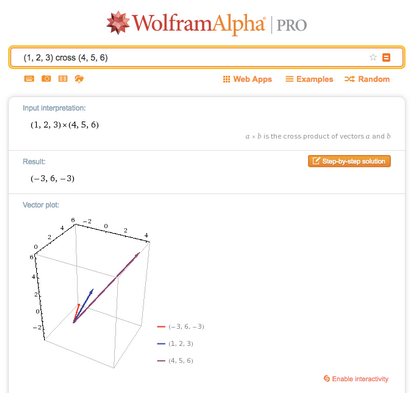
- Le produit vectoriel suit tous les « interactions » entre les dimensions transversales
- Il y a 6 interactions (2) dans chaque dimension, avec des signes en fonction de l'ordre de xyzxyz
Connexion avec le Déterminant
Vous pouvez calculer le produit croisé en utilisant le facteur déterminant de cette matrice:
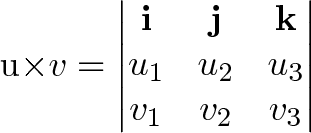
Il y a une connexion propre ici, comme le déterminant ( « zone / volume signé ») suit les contributions des composantes orthogonales.
Il y a des raisons théoriques pour lesquelles le produit croisé (comme un vecteur orthogonal) est uniquement disponible en 0, 1, 3 ou 7 dimensions. Cependant, le produit vectoriel en tant que numéro unique est essentiellement le déterminant (une zone signée, le volume ou hypervolume comme un scalaire).
Connexion avec Curl
Curl mesures de la force de torsion d'un champ de vecteurs applique à un point, et est mesuré avec un vecteur perpendiculaire à la surface. Chaque fois que vous entendez « vecteur perpendiculaire » commencer à penser « produit croisé ».
Nous prenons le « déterminant » de cette matrice:
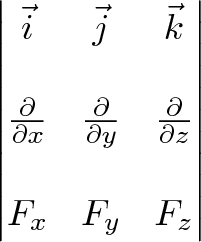
Au lieu de la multiplication, l'interaction prend un dérivé partiel. Comme précédemment, le VEC (i) le composant de boucle sont basées sur les vecteurs et les dérivés de la VEC (j) et (k) vec directions.
Relation avec le théorème de Pythagore
La croix et produit scalaire sont comme les côtés orthogonaux d'un triangle:
Pour les vecteurs unitaires, où | a | = | B | = 1. Nous avons:
Je triché un peu dans le diagramme de la grille, nous devons suivre les grandeurs au carré (comme cela se fait dans le théorème de Pythagore).
Le produit cross - amis à Clifford une prolongation algèbre et algèbre géométrique. Je suis encore à apprendre ces derniers.
Croix Produits de la Croix-Produits
Parfois, vous avez un tel scénario:
Tout d'abord, le produit croisé n'est pas associative. questions d'ordre.
Ensuite, rappelez-vous ce que fait le produit croisé: trouver des vecteurs orthogonaux. Si deux composants sont parallèles (VEC (a) parallèle à vec (b)), alors il n'y a pas de dimensions de poussée sur l'autre, et le produit vectoriel est égal à zéro (qui porte jusqu'à 0 fois vec (c)).
Mais il est ok pour VEC (a) et VEC (c) être parallèles, car ils ne sont jamais impliqués directement dans un produit croisé, par exemple:
Whoa! Comment as-nous rentrerons à VEC (j). Nous avons demandé une direction perpendiculaire à la fois vec (i) et vec (j). et fait que la direction perpendiculaire à vec (i) à nouveau. Être « doublement perpendiculaire » signifie que vous êtes de retour sur l'axe d'origine.
Dot Produit de la Croix-Produits
ce qui se produit? Nous sommes obligés de faire VEC (a) fois VEC (b) Tout d'abord, parce que VEC (b) · VEC (c) renvoie un scalaire (numéro unique) qui ne peut pas être utilisé dans un produit croisé.
Si VEC (a) et VEC (c) sont parallèles, ce qui se passe? Bien, VEC (a) fois vec (B) est perpendiculaire à vec (a). ce qui signifie qu'il est perpendiculaire à vec (c). de sorte que le produit scalaire avec vec (c) est égale à zéro.
Je ne ai jamais vraiment mémorisé ces règles, je dois penser à travers les interactions.
D'autres systèmes de coordonnées
Le moteur de jeu Unity est gaucher. OpenGL (et la plupart des outils mathématiques / physique) sont droitiers. Pourquoi?
Dans un jeu d'ordinateur, x va horizontale, y va vertical et z va « dans l'écran ». Il en résulte un système gaucher. (Faites un essai: à l'aide de la main droite, vous pouvez voir x croix y doit pointer sur l'écran).
Applications du produit Cross
- Trouver la direction perpendiculaire à deux vecteurs donnés.
- Trouvez la zone signée enjambé par deux vecteurs.
- Déterminer si deux vecteurs sont orthogonaux (vérification d'un produit scalaire de 0 est probablement plus rapide si).
- « Multiplier » deux vecteurs quand seulement perpendiculaires termes croisés apportent une contribution (comme la recherche de couple).
- Avec les escouades (4d nombres complexes), le produit croisé effectue le travail de rotation un vecteur autour d'un autre (un autre article dans les œuvres!).
Vote pour 1 Vote contre Répondre
Il y a 1 an 10 mois
Voter 0 Vote contre Répondre
Il y a 1 an 10 mois
quantités w = fa pourquoi scalaires