Colonne de fonction de l'AMS
introduction
de l'essai sur la `mesure d'un cercle d'Archimède est souvent appelé, mais je soupçonne que, peu lu. Ce que la plupart des écrivains modernes intéresse est la prescription pour l'approximation $ \ pi $ en tenant compte des polygones avec un grand nombre de côtés, et la recette récursif il a développé pour ce faire. Cette technique littéralement le tour du monde, et était celui utilisé par tout le monde pour calculer $ \ pi $ jusqu'à ce que la formule en termes d'une série est devenu bien connu. La procédure d'Archimède est pas exactement le même que celui qu'il est généralement cité comme présentation. Le meilleur compte en termes modernes que je connais est dans le livre $ \ pi $ déchaîné.
L'énoncé du théorème d'Archimède
L'essai d'Archimède se décline en deux parties. La première est une déclaration et la preuve d'une relation entre la surface d'un cercle et sa circonférence. Le deuxième se rapproche de $ \ pi $ en appliquant les techniques prévues dans la preuve de cette première partie. Je serai concerné que le premier bien, comme je le dis, il est le deuxième qui attire plus d'attention.
Dans la version de `mesure du cercle » que nous avons maintenant, la déclaration d'ouverture est la suivante:
La superficie de tout cercle est égale à un triangle rectangle dont l'un des côtés sur l'angle droit est égal au rayon, et l'autre à la circonférence, du cercle.
Grosso modo, la raison pour laquelle le théorème est vrai est que nous pouvons tailler à la fois le cercle et le triangle dans des régions très petites qui se rapprochent les uns des autres dans la zone de près:
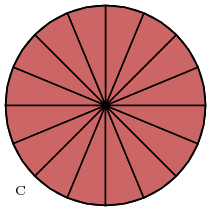
La preuve de ce théorème dans la version existante suit immédiatement sa déclaration. Je vais esquisser ci-dessous, avec un peu d'explication et quelques chiffres ajouté. L'idée de base est presque exactement la même que celle de la preuve d'Euclid du théorème XII.2, qui affirme que (en termes modernes) la surface d'un cercle est proportionnelle au carré de son rayon. Dans la preuve d'Euclid l'aire d'un cercle est délimité au-dessus et au-dessous par les zones de polygones circonscrits et inscrits avec un nombre croissant de côtés, tandis que dans celui de Archimedes la circonférence est de même aussi limitée. Le chevauchement des Archimedes argument avec celui d'Euclide ne devrait pas être surprenant, puisque le théorème de XII.2 d'Euclide est une conséquence immédiate d'Archimède.
La preuve du théorème d'Archimède
Soit $ C $ soit un cercle, $ T $ soit le triangle dont la hauteur est le rayon du cercle et dont la base est de sa circonférence. La preuve à venir est en deux parties, comme toutes les preuves par la méthode de l'épuisement que je suis au courant. Dans le premier, il est démontré que la zone de $ C $ ne peut pas être supérieure à celle de $ T $, et dans la seconde qu'il ne peut pas être moins. Cela ne laisse que la possibilité que les deux zones sont les mêmes
Partie I. Je vais montrer d'abord que la zone du cercle ne soit pas supérieure à la superficie de $ T $. Nous allons avoir besoin de trois faits dans l'argument à venir, dont la preuve que je remets.
Selon la revendication (1) La surface de tout polygone inscrit dans le cercle est inférieur à celui de $ C $.
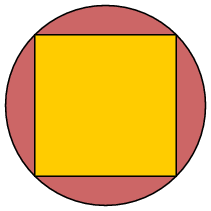


Par (1) la zone de $ \ $ Pi_ est inférieure à celle de $ C $. Laissez $$ \ delta_ = \ hbox< area of > C - \ hbox< area of > \ Pi_> 0 \. $$
Dans les chiffres ci-dessus, $ \ delta_ $ est affiché comme les zones rouges. maintenant vient
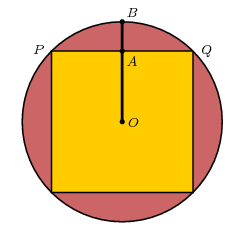
Selon la revendication (3) La surface de tout polygone inscrit dans le cercle est inférieur à celui de $ T $.
Ceci est un peu plus difficile à illustrer. Étant donné que le polygone et le polygone $ T $ peut être partitionné bien, dans le tableau suivant, il découle des revendications qui (a) la PBQ de $ arc $ est plus long que le segment $ PAQ $, et (b) le segment OA $ $ est plus court que $ OB $. Le second résulte de Euclid III.2, qui affirme que le segment PQ $ $ se situe à l'intérieur du cercle. La première est évidente dans l'image, mais nous verrons plus loin qu'il ya des problèmes impliqués à croire ce que vous voyez.
Maintenant, pour l'argument, en supposant que ces réclamations est vrai. Supposons, contrairement à ce que nous voulons prouver que la zone de $ C $ est supérieur à celui de $ T $: $$ = d \ hbox< area of > C - \ hbox T> 0 \. $$
une contradiction avec le choix de $ n $.
Partie II. Dans la seconde moitié de l'argument, nous arrivons à une contradiction en supposant la zone de $ C $ à être inférieur à celui de $ T $, mais cette fois en utilisant des polygones circonscrits. La possibilité ne reste que la zone de $ C $ est le même que la zone de $ T $, ce qui est ce que nous voulions prouver.
Donc, dans cette partie, soit $ \ Pi_ soit $ un carré circonscrivant le cercle $ C $, et en général soit $ \ Pi_ $ soit le polygone régulier de 2n $ côtés $ obtenu à partir de $ \ Pi_ $ en coupant demi-arcs sur $ C $. Dans ce cas $ \ Pi_ $ est strictement contenue dans $ \ Pi_ $ et contient $ C $. Laissez $$ \ delta_ = \ hbox< area of > \ Pi_ - \ hbox< area of > C> 0 \. $$
Selon la revendication (4) La superficie de $ T $ est inférieure à celle de $ \ $ Pi_.
A partir de là l'argument est très similaire à celle de la partie I, déduire une contradiction de l'hypothèse que la zone de $ C $ est inférieur à celui de $ T $.
Il reste à examiner les demandes (1) - (4). Le tout est plus simple (1). Il découle directement de 5 notion commune Livre I ( `l'ensemble est supérieure à sa part») savent une fois qu'un polygone construit à partir de segments coupant des arcs de cercle est contenu dans le cercle. Ceci est exactement ce que III.2 affirme Euclide.
Quelle est exactement la longueur de la circonférence?
Il n'y a pas de place dans Euclide où il parle de la durée de quoi que ce soit, mais un segment de ligne. Nous savons maintenant que cela en fait potentiellement une question très difficile, car il y a des courbes continues bornées dans le plan qui ont une longueur infinie. Bien sûr, la circonférence d'un cercle est pas un de ceux-ci. Le problème vient à ceci: comment peut-on comparer les longueurs des deux courbes dans le plan, ou deux surfaces en trois dimensions? Avec des zones dans le plan, la réponse est relativement simple - on dispose finalement des choses si une zone est contenu dans l'autre. Mais avec des courbes cela est impossible, donc il n'y a pas de réponse évidente vraiment à la question, `` Dans quelles circonstances peut-on dire facilement si une courbe est plus ou moins qu'un autre? » Comment avez affaire Archimedes le problème?
Le problème a surgi d'abord dans ce qui est peut-être l'œuvre la plus célèbre de Archimedes, `Sur la sphère et cylindre I », dans lequel il calcule la surface d'une sphère en le comparant à un cylindre englobante. Ceci est une notion plus complexe que celle de la longueur de la circonférence d'un cercle, mais il est similaire. Dans l'introduction de `Sphère et le cylindre », il formule deux axiomes qui sont exactement ce dont il a besoin ici, bien qu'il ne va pas dans les détails, ou justifier ses formulations. D'une certaine manière ce que les difficultés esquive, mais en même temps, il est très intelligent - il concentre les difficultés dans deux demandes relativement simples, en effet les remettre à plus tard.
La première des axiomes d'Archimède est la comparaison plus simple des courbes possibles.
Axiom 1. Le segment de droite entre deux points est plus court que tout autre chemin entre eux.
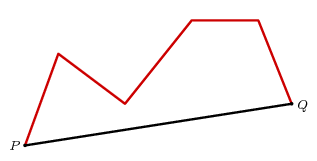
La seconde est plus subtile.
Axiom 2. Supposons que deux points $ P $ et $ Q $ à donner. Supposons que deux chemins de $ P $ à $ Q $ sont données, qui sont tous deux arcs concaves d'un côté du segment PQ $ $. Si l'un d'eux est contenu à l'intérieur de la région délimitée par l'autre et le segment de ligne à partir de $ P $ $ $ Q, il est le plus court.
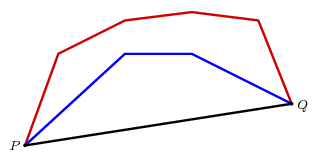
Un chemin de $ P $ à $ Q $ qui se trouve sur un côté du dit $ $ PQ soit concave si la région délimitée par le chemin d'accès et le segment PQ $ $ est convexe. Pour autant que je sache, ce fut d'abord utilisé Archimedes qui ce en mathématiques.
Je vais discuter de ces axiomes en un instant, mais d'abord permettez-moi de montrer comment la revendication (3) suit. Dans notre figure originale du triangle $ T $ divisé en petits triangles, chacun des petits triangles a la base égale à la longueur de la PBQ $ arc $ dans l'image suivante, alors que chaque hauteur est $ OP $. Mais par Axiome 1 la longueur de la PBQ de $ arc $ est supérieur à $ PQ $, alors qu'il suit d'Euclide que $ OB III.2 $ est supérieur à $ OA $. L'application de symétrie, ce qui implique la revendication (3) dans ce cas, et doit indiquer comment le raisonnement va en général.
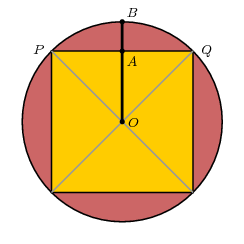
Axiome 2 est utilisé dans la partie II de la preuve du théorème d'Archimède.
Maintenant, on se demande, comment Archimedes ne se convaincre des Axiomes ci-dessus?
Ce qui justifie les axiomes d'Archimède?
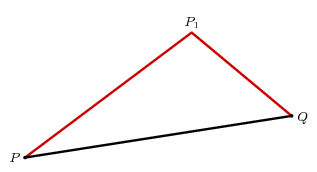
Regardons d'abord Axiom 1. Dans le cas le plus simple, on affirmer que dans un triangle de la longueur d'un côté est inférieur à la somme des longueurs des deux autres côtés. C'est Euclid I.21, et constitue la base de la preuve des cas restants, qui procède par induction, qui connaissait sur une base informelle à Euclide. Supposons par exemple que nous donne un chemin polygonal $ P_, $ P_ $, $ P_, $ P_ = Q $ de trois segments de $ P $ à $ Q $. Dessiner le segment $ P P_ $ et appliquer Euclide I.21: $$ PQ < PP_ + P_Q < (PP_ + P_P_) + P_Q \. $$

Et ainsi de suite, comme Euclide pourrait-on dire.
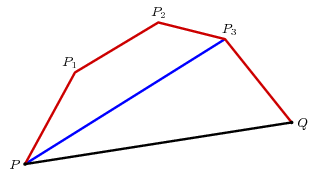
Axiome 2 est plus intéressant. Encore une fois, regardez un cas simple, dans laquelle la courbe intérieure était composée de deux segments.
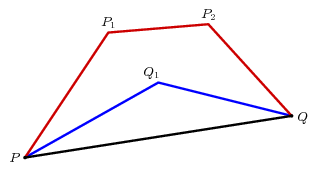
Nous voulons savoir que la longueur de la voie intérieure est inférieure à celle du chemin extérieur: $$ PQ_ + Q_Q < PP_ + P_P_ + P_Q \. $$
L'astuce consiste à prolonger $ PQ_ $ à $ R $, l'intersection de la ligne $ $ PQ_ avec le chemin supérieur. Ce point existe et est unique précisément parce que (a) l'intérieur du chemin fermé $ PP_P_QP $ est convexe et (b) $ PQ_ $ se trouve à l'intérieur.

L'application Axiom 1 nous obtenons deux fois $$ \ EQAlign < PR -< PP_ + P_P_ + P_R \cr Q_Q -< Q_R + RQ \cr PQ_ + Q_Q -< PQ_ + Q_R + RQ \cr -= PR + RQ \cr -< PP_ + P_P_ + P_R \. > $$
En général, on peut appliquer l'induction sur le nombre de segments dans le chemin intérieur, comme la figure à gauche indique:
- Archimedes, `Sphère et cylindre I « et `mesure du cercle », dans la traduction de T. L. Heath des travaux d'Archimède. Publié par Cambridge University Press en 1897, réédité par Dover.
La version de l'essai sur le cercle qui était disponible J. L. Heiberg (dont l'édition sur le grec Heath basé sa traduction) était un peu désorganisé. Il est dit être une copie de ce travail par Reviel Netz, mais je ne sais pas le Archimedes Codex en cours d'édition (lentement) si elle est bien différente de ce que Heiberg et Heath avaient à portée de main.
Euclide, les éléments. Traduit en anglais par T. L. Heath, publié par Cambridge University Press, et réédité par Dover.
Otto Toeplitz, le calcul: une approche génétique. University of Chicago Press, 1963.
Ce livre a été produit à partir d'un manuscrit assez complet trouvé après la mort de l'auteur. Il est un peu trop excentrique pour un texte pratique de calcul, ce qui est ce que l'auteur semble avoir voulu, mais il est très original et souvent brillante. Le chapitre I commence par une discussion sur la façon dont les anciens Grecs traitées processus infinis, et est l'un des rares endroits dans la littérature moderne, où l'on peut trouver une discussion intelligente sur la façon dont ils ont pensé des limites. Il était de ce livre que j'ai appris sur la méthode de l'épuisement.
L'entrée sur Wikipédia Madhava et la série pour $ \ pi $ découverts par les mathématiciens du Kerala.
Cette partie de l'histoire est absente du livre par Arndt et Haenel.
Bienvenue à la
Colonne de fonction!
Recherche Colonne Feature
Colonne de fonction à un coup d'oeil