Comment faire des distributions normales Calculs
Ce guide vous montrera comment calculer la probabilité (aire sous la courbe) d'une distribution normale. Il va d'abord vous montrer comment interpréter un tableau de distribution normale standard. Il vous montrera comment calculer le:
Nous avons une calculatrice qui calcule les probabilités fondées sur des valeurs z pour toutes les situations ci-dessus. De plus, il transmet également tous les travail pour arriver à la réponse, vous savez la logique de la façon de calculer la réponse. La calculatrice peut être trouvée ici.
Comment utiliser le tableau de distribution normale standard
La forme la plus courante de la table de distribution standard normal que vous voyez est un tableau similaire à celui ci-dessous (cliquez sur l'image pour l'agrandir):
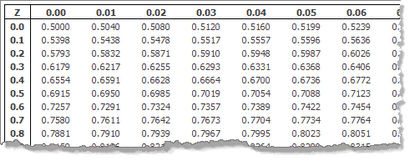
Le tableau de distribution normale standard
Le tableau de distribution normale standard fournit la probabilité qu'une variable aléatoire normalement distribué Z, avec une moyenne égale à 0 et une variance égale à 1, est inférieur ou égal à z. Il fait cela pour des valeurs positives de z seulement (à savoir des valeurs de z sur le côté droit de la moyenne). Ce que cela signifie en pratique que si quelqu'un vous demande de trouver la probabilité d'une valeur étant inférieure à une valeur z spécifique, positive, vous pouvez simplement regarder cette valeur dans la table. Nous appelons ce domaine Φ. Ainsi, pour ce tableau, P (Z a) est la même que la probabilité inférieure à # 150; un
Faire cette connexion est très important car à partir du tableau de distribution normale, on peut calculer la probabilité inférieure à « a », comme « un » est maintenant une valeur positive. Imposer P (Z a)
La probabilité de P (Z> a) est: 1 # 150; Φ (a). Pour comprendre le raisonnement derrière ce regard sur l'illustration ci-dessous:
Vous savez Φ (a) et vous savez que la superficie totale sous la courbe normale standard est 1 donc par déduction mathématique: P (Z> a) est la suivante: 1 - Φ (a).
La probabilité de P (Z> # 150; a) est P (a), qui est Φ (a). Pour comprendre cela, nous devons apprécier la symétrie de la courbe de distribution normale. Nous essayons de trouver la zone ci-dessous:
Mais en réfléchissant la zone autour de la ligne médiane (moyenne), nous obtenons les éléments suivants:
Notez que ceci est la zone même taille que la zone que nous cherchons, que nous savons déjà ce domaine, comme nous pouvons l'obtenir directement à partir de la table de distribution standard normale: il est P (Z # 150; a) est P (Z
L'exigence clé pour résoudre la probabilité entre les valeurs z est de comprendre que la probabilité entre les valeurs z est la différence entre la probabilité de la plus grande valeur z et la plus faible valeur z:
Consultez notre calculatrice ici pour obtenir un peu de pratique!