La courbe normale et le Conseil de Galton
La courbe normale et le Conseil de Galton
par Paul Trow
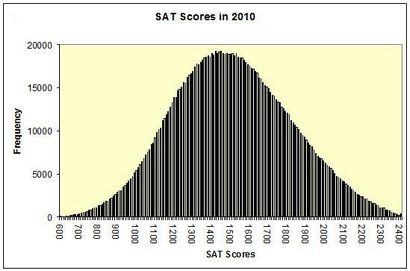
Dans le graphique, la gamme des scores possibles est affiché sur l'axe horizontal. Pour chaque résultat, la hauteur de la barre verticale à ce moment montre le nombre d'étudiants qui ont reçu ce score. Les sommets des barres tracent une forme familière - la normale cuve.
Pourquoi la courbe normale apparaissent souvent dans de nombreux domaines apparemment sans rapport d'étude? Au XIXe siècle, Sir FrancisGalton, l'un des pionniers de la théorie statistique, a inventé un dispositif mécanique qui illustre comment la courbe normale se pose naturellement de la combinaison d'un grand nombre d'événements aléatoires indépendants ou facteurs. Une recréation du dispositif de Galton est illustré ci-dessous.

Le dispositif se compose d'un repères de arrayof montés sur une carte verticale. Lorsque la carte est actionnée, une séquence de billes tombe sur la partie supérieure de la matrice. Quand une balle frappe une épingle, il rebondit à gauche ou à droite avec une probabilité égale, puis tombe au niveau suivant. Lorsque la balle atteint le dernier niveau, il tombe dans l'un des bacs au fond. Comme les billes empiler dans les bacs, ils forment une forme qui ressemble à une courbe normale.
Pour voir une vidéo d'une petite simulation informatique du conseil d'administration de Galton, avec seulement 6 niveaux de broches, cliquez ici.
L'image ci-dessous montre la dernière image de l'animation.
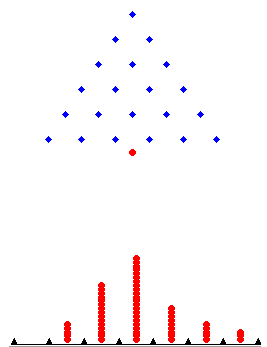
Comme on pouvait s'y attendre, il est plus probable qu'une balle atterrira dans l'un des bacs près du milieu que dans un bac près de l'une des extrémités (0 ou 6). La raison de cela est qu'il ya plusieurs chemins sont une balle peut prendre qui conduisent à des bacs près du milieu que de bacs à proximité des côtés. Pour voir pourquoi, pensez à l'expérience suivante qui simule un chemin aléatoire pour une balle. Jeter une pièce 6 fois et enregistrer la séquence des têtes et des queues que vous obtenez. Si la pièce est i'th Toss la tête, la balle rebondit à droite au niveau i - si le toss i'th est queue, le ballon rebondit sur la gauche. Par exemple, si la séquence de lancers de pièces est H, H, T, H, H, T, la balle prend la pathshown dans le diagramme ci-dessous.
Notez que le nombre de têtes dans cet exemple est 4, et que la balle atterrit dans le numéro bin 4. Si vous essayez quelques exemples, vous pouvez vous convaincre que pour toute séquence de lancers de pièces, le nombre du bac la balle atterrit dans est toujours égal au nombre de fois que la pièce arrive têtes. Par conséquent, le nombre de chemins vers le numéro de bac 4 est le nombre de séquences de 6 lancers de pièces qui ont exactement 4 têtes. Il se trouve qu'il ya 15 telles séquences. (Si vous ne croyez pas, essayez de les écrire.)
D'autre part, il n'y a qu'un seul chemin Tobin 0, correspondant à la séquence de toutes les queues, ce qui signifie que le ballon rebondit vers la gauche à chaque niveau. En conséquence, une balle est 15 fois plus susceptibles d'atterrir dans le bac 4 à 0 bin.
Pour trouver la probabilité qu'une balle atterrira dans le bac i, vous divisez le nombre de chemins bin i par le nombre total de chemins de bins.The tout dernier nombre est 2 6 = 64, becausethe balle peut rebondir dans l'une des 2 façons à chaque niveau et il existe 6 niveaux. Le tableau ci-dessous indique le nombre de chemins à chaque bac, et les probabilités qu'une balle atterrira dans un bac donné.
La figure ci-dessous montre les probabilités graphiquement.
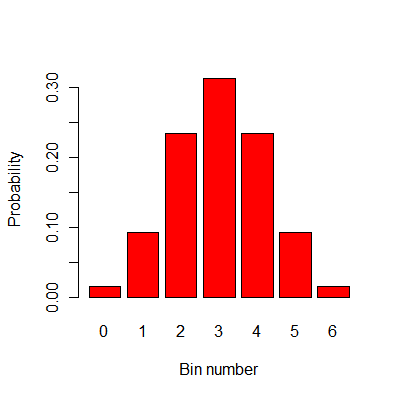
La distribution binomiale et l'approximation normale
Cette répartition des probabilités dans le indiquées dans le tableau et graphique ci-dessus est un cas particulier de la distribution binomiale. La distribution binomiale générale a deux paramètres:
- n - le nombre de lancers de pièces
- p - la probabilité que la pièce viendra tête toute une Toss donnée.
La distribution binomiale donne la probabilité d'obtenir exactement les têtes de k en lancers de pièces de n, pour chaque entier k compris entre 0 et n. Dans l'exemple ci-dessus, n = 6 et la probabilité p = 0,5 - en d'autres termes, la pièce de monnaie est juste.
Les exemples ci-dessus montrent pourquoi la distribution du conseil d'administration de ballsin Galton a la forme d'une distribution binomiale. Mais whatdoes cela a à voir avec la courbe normale? La réponse est que, pour n grand, une variable aléatoire binomiale, withparameter p = 0,5, a approximativement la même distribution que la variable normalrandom avec le même « forme » - qui est, de la même moyenne et l'écart-type. Ceci est un cas particulier d'un résultat célèbre appelé théorème central limite.
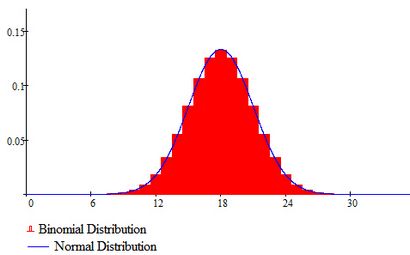
Il se trouve qu'une variable aléatoire binomiale de paramètre p = 0,5 a moyenne n / 2 et l'écart type .Par exemple, si n = 36, la moyenne est de 18 et l'écart type est égal à 3. Le graphique ci-dessous montre la distribution binomiale de ceux-ci paramètres, togetherwith une courbe normale de moyenne 18 et l'écart type 3.
Enfin, voici une photo de la carte réelle Galton construit, qui existe encore à l'University College, Londres. Les balles qui ont abandonné par les broches ont été effectivement tiré de plomb.
