Comment LINEST () Excel Poignées Colinéarité, InformIT
De l'auteur
De l'auteur
Il n'est pas rare, en fait, il est l'état normal des affaires, pour les variables prédictives dans une équation de régression multiple à être corrélées entre elles. Supposons que vous enquêtaient sur le rapport entre le revenu comme une variable de résultat et de l'âge et des années d'éducation comme variables prédictives.
Vous vous attendez à l'âge de corrélation positive avec des années d'éducation. Vous ne vous attendez pas une corrélation parfaite de 1,0 entre les deux variables, mais vous n'êtes pas du tout surpris de trouver une corrélation modérément forte, quelque chose le long des lignes de 0,7.
Une analyse de régression multiple en général (et la fonction DROITEREG () d'Excel en particulier) est parfaitement capable de traiter avec des variables prédictives corrélées (ce que les termes Excel les valeurs x. distincte de valeurs y de la variable de résultat).
Troublesome Colinéarité
Mais il y a un problème quand dépend complètement une des variables prédictives sur un ou plusieurs des autres facteurs prédictifs. Dans ce cas, les approches traditionnelles de génération de l'équation de régression multiple (et la qualité de l'ajustement des statistiques telles que R 2) sont ininterprétable ou simplement faux. Voir la Figure 1 pour un exemple.
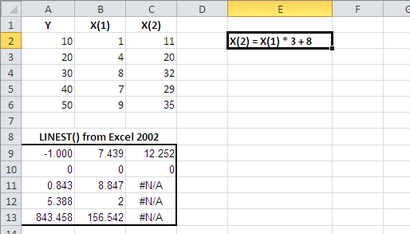
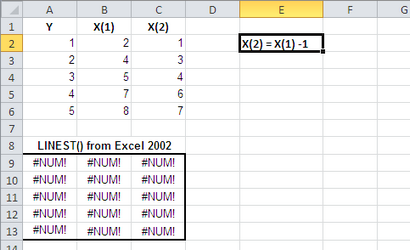
Dans la figure 2, le problème est que la colinéarité provoque la matrice du produit X'X ne pas avoir de inverse (il a un facteur déterminant de zéro), et donc aucune des statistiques de régression peut être calculée en utilisant des approches traditionnelles.
Les « approches traditionnelles » je mentionne dans le paragraphe précédent doivent faire avec des techniques assez simples de l'algèbre matricielle: la transposition de la matrice, la multiplication et l'inversion (même si aucun processus d'inversion de matrice doit être appelée « simple » si plus de trois variables sont impliquées).
De nombreux statisticiens considèrent les erreurs comme tout à fait insignifiant et typique de ce que Freud, dans un contexte différent, appelé le « narcissisme des petites différences ».
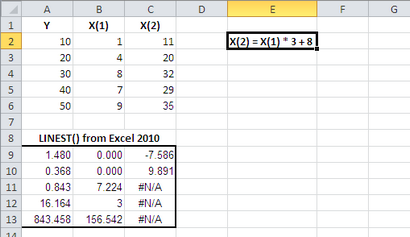
Figure 3 La LINEST () équation de régression renvoie les erreurs-types de non-zéro une exception.
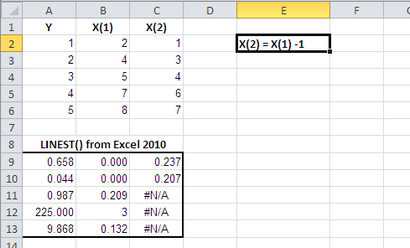
Figure 4 LINEST () renvoie des résultats numériques plutôt que d'une matrice de valeurs d'erreur.
Notez que dans les deux figures 3 et 4 que l'une des variables a une valeur zéro à la fois pour le coefficient de régression (B9 cellulaire dans les deux figures) et de son erreur standard (B10 de cellules dans les deux figures). C'est la manière d'Excel de communiquer à l'utilisateur que, dans ces cas, il considère la variable X (1) dans les deux cas comme une contribution aucune information unique dans l'estimation de Y.
Par conséquent, LINEST () assigne X (1) un coefficient de régression de 0,0, ce qui équivaut à supprimer X (1) à partir de l'équation de régression:
# 374; = -7,586 + 0,0 * X (1) + 1,480 * X (2)
Lorsque vous multipliez X (1) par zéro pour tous les enregistrements, X (1) a abandonné l'équation. Si X (1) dépend entièrement de X (1) -ou vice-versa, alors l'information dans l'une des variables est complètement redondante et un d'entre eux doit être omis de l'équation.
Les variables X (1) et X (2) dépendent parfaitement sur une autre. X (2) est juste X (1) moins 1 - ou, si vous préférez, X (1) est juste X (2) plus 1. Par conséquent, X (1) ne peut fournir aucune information sur Y, une fois que les informations contenues dans Y attribuable à X (2) a été pris en compte.
La dépendance complète en X (1) et X (2) signifie que le choix des variables à déposer à partir de l'équation de régression est informatiquement arbitraire. Ici, Excelle algorithme choisit d'abandonner X (1). Du point de vue de l'interprétation des résultats, vous pourriez ne pas considérer le choix arbitraire.
Indication, par ailleurs, que l'omission de l'une des variables X se reflète dans les degrés de liberté (df) pour le résidu, dans la cellule B12 dans les deux figures 3 et 4. Le résidu df est le nombre de cas moins la nombre de variables prédictives. Il y a cinq cas, un en rangées 2 à 6. Après une omission des variables dépendantes X, il y a une variable X à gauche sur la feuille de calcul. Parce que le troisième argument de DROITEREG () a été omis, la même que la mise à TRUE -Excel fournit automatiquement une colonne de 1 pour représenter la constante. Ainsi, 5 cas moins la variable X restant sur la feuille de calcul, moins la colonne invisible de 1 de pour représenter les feuilles constantes 3 degrés de liberté, tel que rapporté par LINEST ().
Un diagnostic difficile
La dépendance des variables X ne doit pas être limitée à deux des variables, tels que le cas où la variable X (2) est le résultat de la multiplication de la variable X (1) par une constante. Dans ce genre de situation, une simple analyse de corrélation révèle la dépendance. Voir Figure 5.
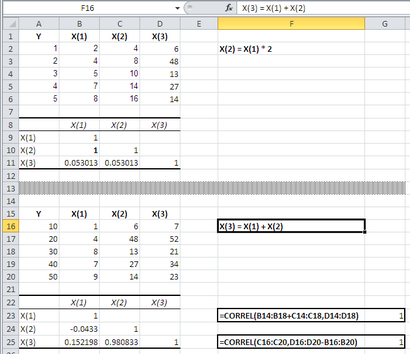
Figure 5 La dépendance est clair à partir de la matrice de corrélation en B9: D11, en particulier la cellule B10, mais pas de B23: D25.
Sur la figure 5, la corrélation entre B2: B6 et C2: C6 est à la fois parfaite et évidente à partir de la matrice de corrélation en B9: D11. X (2) est tout simplement deux fois X (1).
Mais il n'y a pas de corrélation d'ordre zéro de 1,0 dans les données présentées dans B16: D20; il n'y a pas de corrélation de 1,0 dans la matrice représentée sur la B23: D25. Ici, X (3) est la somme de X (1) et X (2). Il n'y a pas une corrélation parfaite entre l'une des variables individuelles, mais il est parfait dépendance linéaire entre X (3) et, comme cela est représenté dans les cellules G23 et G25. Pour déterminer que la dépendance existe sans courir LINEST (). vous devez vérifier un déterminant valide de la matrice SSCP.
Pas d'avertissement
Tout cela est sensible et il est l'approche adoptée par les principales applications statistiques telles que SAS, SPSS, et R.
Cependant, ces paquets vont encore plus loin et alerte l'utilisateur avec un message à l'effet qu'il ya une dépendance complète linéaire dans les données sous-jacentes, et que une ou plusieurs variables ont été retirés de l'équation. Ceci est prévenant. Excel fournit à l'utilisateur sans avertissement le long de ces lignes, en dehors des coefficients de régression d'une valeur zéro et les erreurs standard.
Sans la connaissance de ce que Excel pourrait faire si elle rencontre ce genre de dépendance linéaire, l'utilisateur peut ne pas comprendre la raison pour laquelle l'un des coefficients de régression des variables est 0.0, que l'erreur type est donnée par 0,0, et que la df pour le résidu a en conséquence été augmenté de 1.
En outre, la tendance () utilise la même approche pour le calcul de l'équation de régression comme le fait LINEST (). Mais nulle part dans les résultats TREND () est-il évident qu'une variable a été omis de l'équation de régression. Certes, un utilisateur doit toujours organiser et d'examiner les résultats retournés par LINEST () avant d'accepter sans critique les résultats de DROITEREG (). Néanmoins, TREND () est accompagnée d'aucun avertissement à tout ce que quelque chose d'inattendu aurait pu se produire.