Colinéarité, statistiques réelles avec Excel
Par exemple. dans le tableau suivant, X1 est le double X2. Ainsi X T X est singulier. Excel détecte et crée un modèle de régression équivalente à celle obtenue en éliminant simplement la colonne X2.
Fig 1 - Colinéarité
Figure 1 - Colinéarité
Observation. Dans le cas où k = 2, les estimations des coefficients produits par le procédé moins carré se révéler
puis les dénominateurs des coefficients sont nuls et donc les coefficients ne sont pas définis.
Observation. Malheureusement, vous ne pouvez pas toujours compter sur une colonne étant une combinaison linéaire exacte des autres. Même quand une colonne est presque une combinaison linéaire des autres colonnes, une situation instable peut entraîner. Nous définissons maintenant des mesures qui aident à déterminer si une telle situation est susceptible.
Définition 1. La tolérance est 1 -, où
à-dire le coefficient multiple entre xj et toutes les autres variables indépendantes. Le facteur d'inflation de la variance (VIF) est l'inverse de la tolérance.
Observation. La tolérance varie de 0 à 1. Nous voulons une faible valeur de VIF et une valeur élevée de la tolérance. Une valeur de tolérance inférieure à 0,1 est un signal rouge, tandis que des valeurs inférieures à 0,2 peuvent être source de préoccupation.
Fonctions réelles statistiques Excel. Le vrai statistiques sur les ressources contient les deux fonctions suivantes:
TOLERANCE (R1, j) = tolérance de la j-ième variable pour les données dans la fourchette R1; à savoir 1 -
VIF (R1, j) = VIF de la j-ième variable pour les données dans la fourchette R1
Observation. TOLERANCE (R1, j) = 1-Rcarré (R1, j)
Exemple 1. Vérifier la tolérance et de VIF pour les données affichées dans la figure 1 de corrélation multiple (à savoir les données pour les 12 premiers états dans l'exemple 1 de corrélation multiple).
La partie supérieure de la figure 2 montre les données pour les 12 premiers états dans l'exemple 1. A partir de ces données, on peut calculer la tolérance et de VIF pour chacun des 8 variables indépendantes.
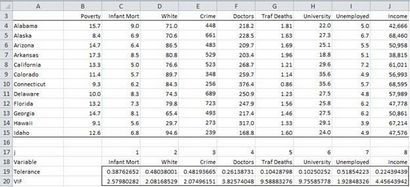
Figure 2 - Tolérance et VIF
Figure 2 - Tolérance et VIF
Par exemple, pour calculer la tolérance pour le crime que nous devons exécuter l'outil d'analyse des données de régression pour les données dans la gamme C4: J15 hors la colonne E comme l'entrée X par rapport aux données de la colonne E comme entrée Y. (Pour ce nous avons d'abord besoin de copier les données afin que l'entrée X se compose de cellules contiguës). On voit alors que plusieurs R carré = 0,518, et donc la tolérance = 1 à 0,518 = 0,482 et VIF = 1 / 0,482 = 2,07.
En variante, nous pouvons utiliser les fonctions supplémentaires TOLERANCE (C4: J15,3) = 0,482 et VIF (C4: J15,3) = 2,07 (puisque la criminalité est la variable 3 e). Les résultats sont présentés dans la partie inférieure de la figure 1. Notez que nous devrions être préoccupés par les décès de la circulation et les variables universitaires puisque leurs valeurs de tolérance sont environ 0,1.
En termes simples, pouvez-vous expliquer le danger multicolinéarité lors de l'exécution de régression linéaire multiple à des fins de modélisation prédictive. Je comprends les questions qu'elle apporte à l'interprétation du modèle (coefficients de paramètres étranges et les valeurs p), mais par rapport à faire des prédictions, ce que dois-je savoir?
Essentiellement, cela signifie que l'une des variables indépendantes est pas vraiment nécessaire au modèle parce que son effet / impact sur le modèle est déjà capturé par quelques-unes des autres variables. Cette variable ne contribue rien supplémentaire aux prévisions et peut être retiré. Le danger est mathématique car il rend le modèle instable dans le sens où un petit changement dans les valeurs de cette variable peut avoir un impact important sur le modèle.
Vous pouvez penser presque 1 / (a-b). Si a et b sont à peu près égale la valeur de 1 / (a-b) est très grande; si a = b, alors sa valeur est non défini (ou infini).
Si vous avez vrai multicolinéarité, la variable « problème » sera automatiquement supprimé par Excel. Le vrai problème se produit lorsque vous n'avez pas multicolinéarité exacte (similaire au cas où a = b), mais proche de multicolinéarité (similaire au cas où est proche de b). Dans ce cas, selon la complexité du modèle de régression, la variable « problème » ne sera pas éliminé, et la situation instable décrit ci-dessus peut entraîner.
Grande explication - très claire, je vous remercie!
J'ai essayé d'entrer VER () et me donner 3.6.2 dans la cellule. (Cela devrait être le numéro de version). Mais encore VIF est pas été calculée.
Mes données présentes dans la gamme A1: K23 avec tête de ligne (ligne 1) et en-tête de colonne (Col A), et la formule je utilise est = VIF (B2: K23,2)
Puis-je joindre un fichier à ce message? Je suis dans la thèse finale du programme de MBA et ce complément pourrait être une aide réelle pour moi. Je vous remercie.
» Erreur du compilateur dans le module caché »
et se traduit par erreur de valeur. S'il vous plaît guider ce que je fais mal.
Je vous remercie.
Faseeh
Faseeh,
Essayez d'entrer la formule = VER () dans une cellule vide dans une feuille de calcul. Si vous obtenez une erreur, le complément n'a pas été installé correctement. Si vous obtenez le numéro de version (par exemple 3.6.2) des statistiques réelles complément alors la cause est différente et nous aurons besoin de diagnostiquer le problème d'une manière différente.
Charles