Comment prouver que Triangles isométriques - SSS, SAS, ASA, règles AAS (solutions, exemples, vidéos)
congruentes Triangles
triangles congruents sont des triangles qui ont la même taille et la forme. Cela signifie que les côtés correspondants sont égaux et les angles correspondants sont égaux.
On peut dire si deux triangles sont congruents sans tester tous les côtés et tous les angles des deux triangles. Dans cette leçon, nous allons examiner les quatre règles pour prouver la congruence triangle. Ils sont appelés la règle SSS, règle SAS, règle ASA et règle AAS. Dans une autre leçon, nous allons considérer une preuve utilisée pour des triangles rectangles appelés la règle Leg hypoténuse. Tant que l'une des règles est vrai, il suffit de prouver que les deux triangles sont congruents.
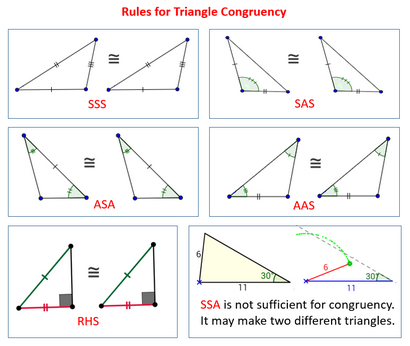
Les schémas ci-dessous montrent les règles de Triangle congruence: SSS, SAS, ASA, AAS et RHS. Prenez note que l'Afrique subsaharienne ne suffit pas pour Triangle congruence. Faites défiler la page pour plus d'exemples, des solutions et des preuves.
Side-Side-Side (SSS) Règle
-Side-Side est une règle utilisée pour prouver si un ensemble de triangles donné sont congruents.
La règle SSS stipule que:
Si les trois côtés d'un triangle sont égaux à trois côtés d'un autre triangle, alors les triangles sont congruents.
Dans les schémas ci-dessous, si AB = RP. BC = PQ et CA = QR, alors le triangle ABC est conforme au triangle RPQ.
Side-Angle-Side (SAS) Règle
Side-Angle-Side est une règle utilisée pour prouver si un ensemble de triangles donné sont congruents.
La règle SAS affirme que
Si deux côtés et l'angle inclus d'un triangle sont égaux à deux côtés et d'un autre angle inclus triangle, alors les triangles sont congruents.
Un angle inclus est un angle formé par deux côtés donnés.
Inclus Angle Angle non-inclus
Pour les deux triangles ci-dessous. si AC = PQ. BC = PR et de l'angle C = angle P, puis en utilisant la règle SAS, triangle ABC est congru à triangle QRP
Angle-Side-Angle (ASA) Règle
Angle côté-angle est une règle utilisée pour prouver si un ensemble de triangles sont congruents donné.
La règle ASA précise que
Si deux angles et le côté d'un triangle inclus sont égaux à deux angles inclus et latérale d'un autre triangle, alors les triangles sont congruents.
Angle-Angle-Side (AAS) Règle
Angle côté-angle est une règle utilisée pour prouver si un ensemble de triangles sont congruents donné.
La règle stipule que l'AAS
Si deux angles et un côté non-inclus d'un triangle sont égaux à deux angles et un côté non-inclus d'un autre triangle, alors les triangles sont congruents.
Dans les schémas ci-dessous, si AC = QP. angle A = Q. angle et l'angle B = angle R, alors le triangle ABC est congru à triangle QRP.
Trois façons de prouver congruent triangles
Une leçon sur SAS, ASA et SSS.
1. SSS Postulate: S'il existe une correspondance entre les sommets de deux triangles de telle sorte que les trois côtés d'un triangle sont congrus sur les côtés correspondants de l'autre triangle, les deux triangles sont congruents.
2. SAS Postulate: S'il existe une correspondance entre les sommets de deux triangles de telle sorte que les deux côtés et l'angle inclus d'un triangle sont congrus pour les parties correspondantes de l'autre triangle, les deux triangles sont congruents.
3. ASA Postulate: S'il sort une correspondance entre les sommets de deux triangles de telle sorte que deux angles inclus et le côté d'un triangle sont congruents aux parties correspondantes de l'autre triangle, les deux triangles sont congruents.
- Afficher étape par étape Solutions
L'utilisation de deux colonnes pour Prouvez Proofs Triangles isométriques
Triangle congruence par SSSComment prouver que Triangles isométriques en utilisant le Postulat Side Side?
Si trois côtés d'un triangle sont congru à trois côtés d'un autre triangle, les deux triangles sont congruents.
- Afficher étape par étape Solutions
Comment prouver que Triangles isométriques en utilisant le SAS Postulat?
Si deux côtés et l'angle inclus d'un triangle sont congrus à deux côtés et l'angle inclus d'un autre triangle, les deux triangles sont congruents.
- Afficher étape par étape Solutions
Prouvez Triangle congruence avec ASA Postulat
Comment Prouvez Triangles isométriques en utilisant l'angle latéral Angle Postulat?
Il deux angles et le côté d'un triangle inclus sont congruents à deux angles et le côté inclus d'un autre triangle, les deux triangles sont congruents.- Afficher étape par étape Solutions
Comment Prouvez Triangles isométriques en utilisant l'angle Angle Side Postulat?
Il deux angles et un côté non-inclus d'un triangle sont congrus à deux angles et un côté non-inclus d'un autre triangle, les deux triangles sont congruents.
- Afficher étape par étape Solutions
Faites pivoter au format de l'écran du paysage sur un téléphone mobile ou petite tablette pour utiliser le widget Mathway, un résolveur de problèmes mathématiques gratuit qui répond à vos questions avec des explications étape par étape.
Vous pouvez utiliser le solveur de la calculatrice Mathway libre et problème ci-dessous pour pratiquer l'algèbre ou d'autres sujets de mathématiques. Essayez les exemples donnés, ou tapez dans votre propre problème et vérifier votre réponse avec les explications étape par étape.Articles Liés