Différenciation (dérivés Recherche)
Différenciation est de trouver les taux de variation d'une quantité par rapport à l'autre. Nous avons besoin de différenciation lorsque le taux de variation est pas constante.
Qu'est-ce que ça veut dire?
Taux de changement constant
Prenons l'exemple d'une voiture roulant à une constante 60 kmh. Le graphique distance-temps ressemblerait à ceci:
On remarque que la distance augmente de point de départ à une vitesse constante de 60 km par heure, donc après 5 heures, nous avons parcouru 300 km. On constate que la pente (gradient) est toujours 300/5 = 60 pour le graphique entier. Il y a un taux constant de changement de la distance par rapport au temps. La pente est positive tout le chemin (le graphique monte au fur et à gauche à droite sur le graphique.)
Continuer la lecture ci-dessous # 8681;
Taux de changement qui est constant
Maintenant, nous allons jeter tout droit dans l'air une balle. Parce que la gravité agit sur la balle, il ralentit, il change de direction et commence à tomber. Tout le temps au cours de cette mouvement la vitesse est en train de changer. Il va de positif (quand la balle va vers le haut), ralentit à zéro, devient alors négatif (comme la balle est en baisse). Au cours de la « up » phase, le ballon a une accélération négative et comme elle tombe, l'accélération est positive.
Maintenant, regardons le graphique de la hauteur (en mètres) contre le temps (en secondes).
Notez cette fois que la pente du graphique change tout au long de la motion. Au début, il a une pente positive forte (ce qui indique la grande vitesse, nous donnons quand on le jette). Puis, comme il ralentit, la pente devient de moins en moins jusqu'à ce qu'il devienne 0 (lorsque la balle est au plus haut point et la vitesse est égale à zéro). Ensuite, la balle commence à baisser et la pente devient négative (correspondant à la vitesse négative) et la pente devient plus raide (comme la vitesse augmente dans le sens négatif).
La pente d'une courbe à un point nous indique le taux de variation de la quantité à ce moment-là.

Concept Important - Approximations de la pente
Maintenant, nous allons effectuer un zoom avant sur la section du graphe près de t = 1 (où j'ai le rectangle dans le graphique ci-dessus). Nous regardons le bit entre t = 0,9 s et t = 1,1 s. Il ressemble à ceci:
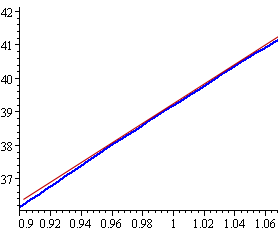
En observant le graphique, on voit qu'il passe à travers (0,9, 36,2) et (1.1, 42). Ainsi, la pente de la tangente à t = 1 est d'environ:
Les unités sont m / s, comme cela est une vitesse. Nous avons trouvé le taux de changement en regardant la pente.
Il est clair que, si nous devions un zoom avant, notre courbe regarderait et nous pourrions même plus droit obtenir une approximation encore mieux pour la pente de la courbe.
Cette idée de « zoomer » sur le graphique et de se rapprocher de plus en plus d'obtenir une meilleure approximation de la pente de la courbe (nous donnant ainsi le taux de changement) a été la percée qui a conduit au développement de la différenciation.
Développement de calcul différentiel
Jusqu'à l'époque de Newton et Leibniz, il n'y avait aucun moyen fiable de décrire ou de prédire cette vitesse en constante évolution. Il y avait un réel besoin de comprendre comment en permanence des quantités variables pourraient être analysées et prévues. Voilà pourquoi ils ont développé le calcul différentiel. que nous apprendrons dans les prochains chapitres.
Les fondateurs de calcul
Pourquoi Différenciation étude?
Il existe de nombreuses applications de différenciation en sciences et en génie. Vous pouvez voir certains d'entre eux dans les applications de différenciation.
La différenciation est également utilisé dans l'analyse des finances et de l'économie.
Une application importante de la différenciation est dans le domaine de l'optimisation. ce qui signifie que la condition de trouver un maximum (ou minimum) de se produire. Ceci est important dans les affaires (réduction des coûts, augmentation des bénéfices) et l'ingénierie (résistance maximale, le coût minimum.)
Exemple d'optimisation
Une boîte avec une base carrée est ouvert vers le haut. Si 64 cm 2 de matériau est utilisé, quel est le volume maximal possible pour la boîte?
Nous reviendrons plus loin sur ce problème et voir comment le faire dans les applications du chapitre de différenciation.
L'approche que nous utilisons
L'approche que nous suivons ici est le même que celui découvert historiquement:
Le reste du chapitre explique comment trouver des dérivés d'expressions plus complexes.
Voir aussi l'introduction au calcul. où il y a un bref historique du calcul.
Nous commençons par quelques informations comment et pourquoi les travaux de différenciation, en: