factorisation
factorisation
Les arbres de facteur
Comme il est mentionné à la séance 14, les nombres premiers sont importants dans la sécurité informatique comme avec Cryptographie à clé publique. Une préoccupation dans la sécurité informatique est la capacité de prendre en compte un grand nombre. L'une des raisons que les ordinateurs peuvent maintenir la sécurité est que de nombreux grand nombre sont difficiles à prendre en compte dans les produits de nombres premiers. quelqu'un doit trouver une méthode pour factoriser facilement tout grand nombre ou pour tester si elle est premier, la sécurité informatique ne serait plus en sécurité. À un moment donné, RSA Laboratories offre des prix monétaires importants pour les problèmes de défi impliquant un grand nombre d'affacturage.
Entier factorisation - Wikipédia, l'encyclopédie libre
RSA Factoring Défi
nombres premiers peuvent être considérés comme les éléments constitutifs des nombres naturels?
Nous savons que 42 = 2 × 3 × 7. Y at-il une autre façon de représenter 42 en tant que produit de nombres premiers?
La seule façon d'écrire 42 comme le produit de nombres premiers (sauf pour changer l'ordre des facteurs) est 2 × 3 × 7. Nous appelons 2 × 3 × 7 la factorisation de 42. Il se trouve que tous les numéros de comptage (naturel nombre) a une factorisation prime unique, différent de tout autre numéro de comptage. Ce fait est appelé le théorème fondamental de l'arithmétique. théorème fondamental de l'arithmétique - Wikipédia, libre.
Prime factorisation peut nous aider à divisibilité, ce qui simplifie les fractions, et de trouver des dénominateurs communs pour les fractions.
Un procédé de production du factorisation d'un nombre naturel est d'utiliser ce qu'on appelle un arbre de facteur.
Exemple: Nous montrons deux façons de construire un arbre de facteur de 24.
Continuer affacturage chaque arbre jusqu'à la fin.
Notez que chaque arbre se termine par la factorisation prime unique de 24 = 2 · 2 · 2 · 3 = 2 3 · 3.
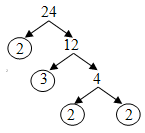
Donc, le premier factorisation de 24 est 24 = 2 · 2 · 2 · 3 = 2 3 · 3.
Une bonne façon de vérifier le résultat est de multiplier le et assurez-vous que le produit est de 24.
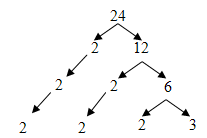
Certaines personnes préfèrent cette méthode parce que chaque niveau multiplie encore le nombre initial, et en faisant baisser les nombres premiers, nous sommes moins susceptibles de les manquer et les laisser hors de notre factorisation.
Notez que la factorisation est encore 24 = 2 · 2 · 2 · 3 = 2 3 · 3, même si nous avons commencé avec 2 · 12 au lieu de 6 · 4.
Problème auto-Check
Faire un autre arbre de facteur de 24, où deux facteurs différents sont utilisés dans la première étape que celles utilisées ci-dessus.
Faire un arbre de facteur pour trouver la factorisation 36.
Pour cette classe, la forme standard d'une factorisation est d'écrire les facteurs dans l'ordre croissant (au plus grand) et d'utiliser la forme d'exposant lorsqu'un facteur est répété avec un point pour symboliser la multiplication.
Exemples: 24 = 2 3 · 3 et 600 = 2 3 · 3 · 5 2
Problème auto-Check
Trouvez la factorisation de 588.
Problème de session 1. (Old Session 1)
Cary, Dana et Pat sont élus pour être président, secrétaire, trésorier et d'un club. Combien de différents résultats des élections sont possibles?
Nous avons résolu ce problème en tirant toutes les correspondances possibles 1-1 entre les personnes et les bureaux. Nous avons pu faire six différentes correspondances 1-1. Plus tard, en session 9 (Old Session 9), nous avons eu le principe de comptage fondamental, qui nous a donné une méthode pour trouver le nombre de possibilités par multiplication: 3 choix pour le président, puis 2 choix pour le secrétaire, et enfin seulement 1 choix pour trésorier . Ainsi, le nombre de possibilités est 3 · 2 · 1 = 6.
Les problèmes de ce type où l'on multiplie descendant des nombres naturels se présentent assez souvent en mathématiques, en particulier dans les probabilités et les statistiques. Ce qui motive un factoriel. qui est une opération pour ce type de multiplication.
Pour évaluer quatre factoriel. on multiplie 4 fois par successivement plus petit nombre naturel, tout le chemin jusqu'à 1. Donc, quatre factoriel est 4! = 4 · 3 · 2 · 1 = 24.
Exemple: 8! = 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 40.320.
Notez que la valeur devient grande assez rapidement.
Nous pouvons trouver la factorisation d'un factoriel en trouvant le premier factorisation de chacun de ses facteurs.
Exemple: 2 7 = 128 doit être un facteur de 8! depuis 2 7 fait partie de la factorisation de 8 !.
Exemple: 10 doit être un facteur de 8! puisque les deux 2 et 5 sont des facteurs principaux de 8 !.
Exemple: 100 est pas un facteur de 8! puisque 100 = 2 2 · 5 2. donc nous avons besoin de deux facteurs de 5 pour obtenir 100 et 8! seulement a un facteur de cinq.
Exemple: 2 2 · 3 2 doit être un facteur de 8! depuis le premier factorisation de 8! contient à la fois deux 2 et deux 3 de.
Problèmes d'auto-contrôle
Trouvez la factorisation pour 6 !.
Laquelle des valeurs suivantes sont des facteurs de 6 !?