Fonctions logarithmiques
Qu'est-ce qu'un journal et pourquoi avons-nous besoin?
Je dois admettre que les journaux sont un de mes sujets favoris en mathématiques. Je ne sais pas exactement pourquoi, mais vous pouvez faire beaucoup de choses impressionnantes avec eux! Nous verrons bientôt que les journaux peuvent être utilisés pour « obtenir la variable dans l'exposant vers le bas » afin que nous puissions résoudre pour cela. Mais logarithmes sont également utilisés pour beaucoup d'autres choses, y compris très tôt pour effectuer des calculs - avant les calculatrices et les ordinateurs étaient autour. Avez-vous déjà entendu parler d'une règle de diapositive? (Demandez à vos parents ...)
Une règle à calcul a été utilisée (entre autres) pour multiplier et diviser un grand nombre en ajoutant et en soustrayant les exposants. Les chiffres sur les règles de diapositives avaient différentes échelles ( « échelles logarithmiques », ce qui signifie que la distance entre le nombre augmente de façon exponentielle) et vous pouvez simplement rechercher un numéro, et faites glisser la règle sur un autre numéro pour obtenir le numéro que vous voulez. Quand vous faites cela, vous ajoutiez et en soustrayant les exposants, multipliant ainsi et en divisant un grand nombre. Génie!
Définition des logarithmes
Rappelez-vous: Un journal est en exposant. Alors, quand vous prenez le journal de quelque chose, vous récupérez un exposant. Les deux équations ci-dessous sont deux façons différentes de dire la même chose, mais la première est une équation exponentielle, et la seconde est une équation logarithmique.
Notez que b est appelée la base du journal, et doit être supérieure à 0 (donc on n'a pas à traiter avec des nombres complexes). En outre, la base ne peut pas être 1. ou les équations ne serait pas exponentielle ou logarithmique.
L'y dans l'équation de log est appelée l'argument et il doit être supérieur à 0. encore, pour éviter des nombres complexes.
Pour illustrer la façon dont ces deux équations sont liées, à plusieurs reprises une « boucle » apparaît, qui montre que b élevé au x est égal à y. Encore une fois, y est appelé l'argument du journal, et vous pouvez l'écrire comme \ (_> x \) ou \ (_> (x) \). Apprenez ce bien!
Remarque. S'il n'y a pas b à côté du journal, la base est supposée être 10.
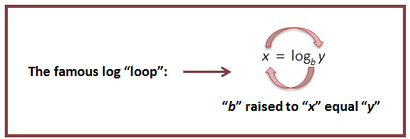
Voici quelques exemples où nous changeons une fonction exponentielle à une fonction de journal, et une fonction de journal à une fonction exponentielle. Voir la boucle?
La plupart des logarithmes que vous allez travailler avec une base ont soit « 10 » (parce que nous allons traiter dans la base 10 avec notre système de comptage) ou la base « e ». Un logarithme de base 10 est appelé un logarithme commun. et quand vous voyez « log » sans un petit indice pour la base, vous assumez est la base 10. Donc \ (\ log \ left (1000 \ right) = 3 \) et \ (_> \ left (1000 \ right) = 3 \), mais on n'a pas besoin du 10. logarithme avec e de base est appelé « logarithme naturel » et est écrit \ (Dans \ gauche (x \ droite) \). Donc nous écrivons \ (_> \ left (x \ droite) \) comme \ (Dans \ gauche (x \ droite) \).
Encore une fois, la base « e » a de nombreuses applications en ingénierie et en économie.
Vous pouvez utiliser les touches de la calculatrice graphique pour trouver les journaux de base: LOG (base 10) et LN. Pour les journaux avec d'autres bases, vous pouvez utiliser une fonction appelée Logbase sous MATH (ou ALPHA FENÊTRE 5), ou utiliser ce que nous appelons une formule « changement de base », que nous allons présenter ici et parler de plus dans les propriétés de base Log ci-dessous . Nous avons appris à mettre les exposants dans la calculatrice (en utilisant ^) ici dans les Radicaux et dans Exponents section algèbre.
Notez que vous pouvez également utiliser votre calculatrice pour effectuer des régressions logarithmiques. en utilisant un ensemble de points, comme nous l'avons fait ici dans la section Fonctions exponentielles.
Voici quelques exemples de graphiques de journal parent. Encore une fois, je me rappelle toujours que le « point d'ancrage » de la fonction exponentielle que nous avons vu plus haut est (avant tout déplacement du graphique) est (0, 1) (depuis le « e » dans « exp » regarde autour comme un « 0 « ), et le « point d'ancrage » d'un functionis log (1, 0) (car cela ressemble à la « lo » dans « log »). Il faut se rappeler aussi que si les changements de fonction, ce « point d'ancrage » se déplace. On notera également que le graphe d'une fonction de log (fonction parental: une qui ne soit pas déplacé) a une asymptote de x = 0.
Ces graphiques parents peuvent être transformés comme les autres graphiques des parents dans la section Fonctions parents et transformations.
Lorsque vous travaillez avec des journaux, il y a certains raccourcis que vous pouvez utiliser encore et encore. Il est important de comprendre ces derniers, mais plus tard, lors de leur utilisation, se familiariser avec eux, afin que vous puissiez les utiliser rapidement. Pensez à quelques-unes des règles « annulant » les journaux avec les exposants. Et ne pas oublier le journal « boucle »:

Maintenant, pour les importantes propriétés du journal. Ces propriétés proviennent du fait que nous ajoutons des exposants lorsque nous multiplions termes avec les exposants. nous soustrayons exposants quand nous divisons. et nous multiplions les exposants quand nous les élever à une puissance. Ce sont des propriétés puissantes que nous aurons besoin d'utiliser pour isoler les variables exposants afin que nous puissions résoudre pour eux. Vous devrez mémoriser ces derniers et se rappeler que pour les trois premiers, vous devez avoir affaire à des journaux avec la même base:

Et ne pas oublier les bases:
Maintenant, nous allons utiliser ces propriétés pour développer et condenser les journaux. L'expansion Logs signifie généralement tournant le « à l'intérieur de la multiplication » (avec un seul log) pour « en ajoutant à l'extérieur » (avec de multiples journaux). Logs moyens de condensation généralement tournant le « extérieur ajoutant » (avec de multiples journaux) à « l'intérieur de multiplication » (avec un seul log).
Pourquoi avons-nous besoin de faire tout cela? Nous aurons besoin d'élargir et de condenser les journaux pour résoudre les problèmes du journal. Notez que lors de l'expansion des journaux, il est généralement une bonne idée d'appliquer la règle de pouvoir dernier (à moins que les termes entiers sont élevés à une puissance, comme dans le troisième exemple). Notez également que ces journaux peuvent être écrits avec ou sans les arguments entre parenthèses (par exemple, comme \ (_> 5 ^> \, \, \, \ texte \, \, \, \, _> \ left (5 ^> \ right) \), qui est différent de \ (_> 5x \ right)> ^> \)).
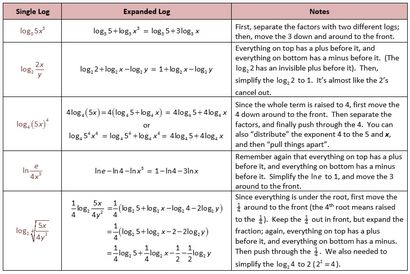
Maintenant, nous allons aller dans l'autre sens. Lorsque la condensation des journaux, il est généralement préférable d'appliquer la règle de la première puissance.
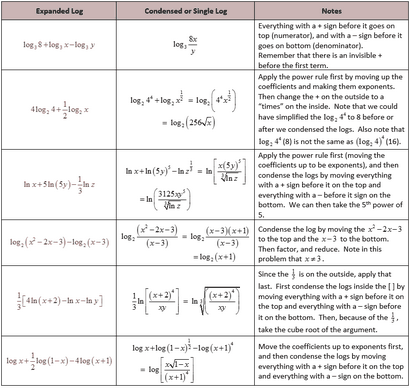
Maintenant, nous pouvons utiliser tous ces outils pour résoudre des équations log! Rappelez-vous encore que les mathématiques est juste en utilisant les outils que vous devez apprendre à résoudre des problèmes.
Rappelez-vous de toujours vérifier votre réponse pour vous assurer que l'argument des journaux (ce qui suit directement le journal) est positif!
Ouvrons juste et d'essayer une résolution. Il existe des moyens de base pour résoudre les problèmes du journal:
1. Utilisez la règle de puissance pour obtenir l'exposant vers le bas si la variable est l'exposant (probablement le plus couramment utilisé « outil »). Avant de le faire, obtenir la base / exposant lui-même et prendre ln ou log de chaque côté. Vous utiliserez généralement quand vous n'avez pas de journaux dans l'équation, mais avoir des variables dans les exposants. Nous utilisons généralement Dans au lieu de journal. à moins que nous avons affaire à la base 10.
Nous pouvons également utiliser le journal avec la base sous l'exposant, comme dans le second cas du premier exemple:
Remarque. Vous pourriez être invité à résoudre des problèmes simples comme ceux-ci en utilisant le journal « boucle » et le changement de formule de base à la place:
2. Si le même journal et même base sont des deux côtés, vous pouvez simplement définir des arguments de journaux égaux les uns aux autres:
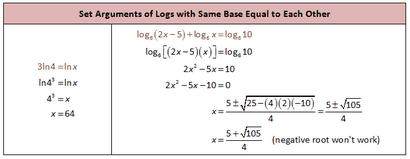
3. Si x est en dessous d'un exposant complexe, soulever chaque côté à l'inverse de ce exposant. Vous utilisez généralement si vous avez des variables soulevées à des exposants. Ceux-ci ne sont pas vraiment enregistrer les problèmes, mais vous les verrez:

5.Ajouter une base pour les deux parties qui est la base de la bille; si vous avez un « ln » dans le problème, utilisez la base « e ». Vous utiliserez généralement quand vous avez des journaux dans l'équation; vous pouvez utiliser au lieu d'utiliser la boucle journal. Certains d'entre eux semblera familier!
Faisons quelques problèmes et voir quelles sont les techniques que nous utilisons:

Voici quelques autres:
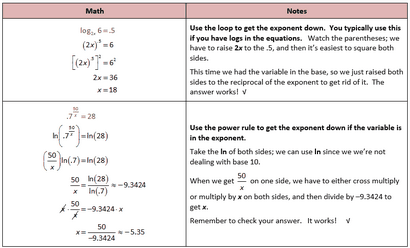
Encore une fois, nous utilisons généralement les journaux pour résoudre des problèmes où nous avons une variable dans l'exposant; nous pouvons utiliser la règle Power pour « obtenir l'exposant vers le bas ».
Nous allons d'abord refaire le problème plus tôt pour voir combien il est facile d'utiliser les journaux que « deviner et vérifier » lorsque la variable est dans l'exposant.
(B) Maintenant, nous pouvons enfin utiliser les journaux au lieu de « Devinez et Check »:
Croissance de la population problème
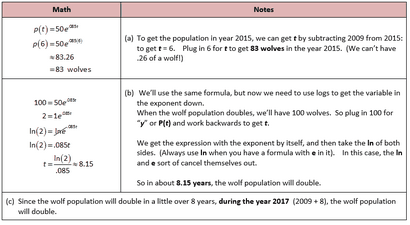
De nombreux problèmes de fois vous donnera la formule exponentielle, et vous avez essentiellement à brancher pour obtenir les réponses:
(B) Combien d'années faut-il pour doubler la population?
(C) Au cours de quelle année doublera la population?
Problème Compounding continue:
Madison veut vraiment acheter une voiture. Elle a besoin d'un acompte de 4 000 $. Si elle dépose 3500 $ maintenant avec intérêt composé en continu à 3%, combien d'années il l'emmener à économiser suffisamment pour acheter la voiture?
Utilisation des journaux pour trouver le problème Tarif:
Une grande colonie de puces est en croissance exponentielle sur le chien de la famille (beurk!). Il y a 400 initialement fuit.
(A) S'il y a 600 puces après 1 jour, combien ce qu'il y aura après 5 jours?
(B) Combien de temps faudra t-il avant il y a 10.000 puces?
Revisiter Half Life problème
Nous pouvons résoudre les problèmes de demi-vie en utilisant deux méthodes différentes; nous allons utiliser les deux méthodes ici. Nous avons résolu un problème demi-vie au-dessus dans la section Exponents, mais si vous avez besoin de trouver un temps (une variable dans l'exposant), alors vous devez utiliser les journaux.
Une substance chimique a une demi-vie de 6 heures.
(A) Combien d'un échantillon de 40 grammes reste après 18 heures?
(B) Combien de temps jusqu'à ce qu'il n'y a que 2 grammes gauche?
Solution (Méthode 1, comme nous l'avons utilisé dans la section Fonctions exponentielles):
Solution (Méthode 2):
Parfois, vous apprendrez à résoudre un problème demi-vie en utilisant le \ (A = P ^> \) formule et obtenir le k d'abord, comme nous l'avons fait dans le problème de puces plus tôt. Cette méthode semble un peu plus difficile, mais parfois vous demande de l'équation demi-vie avec le k en elle.
Apprenez ces règles et la pratique, la pratique, la pratique!
Pour s'entrainer. Utilisez le widget Mathway ci-dessous pour essayer un condensant un problème journal. Cliquez sur Soumettre (la flèche bleue à droite du problème) et cliquez sur Write comme Logarithme unique pour voir la réponse.
Vous pouvez également saisir votre propre problème, ou cliquez sur les trois points dans le coin supérieur droit et cliquez sur « Exemples » pour forer vers le bas par sujet.
Si vous cliquez sur Touchez pour afficher les étapes. ou cliquez ici. vous pouvez vous inscrire à Mathway pour un essai gratuit. puis passer à un abonnement payant à tout moment (pour obtenir tout type de problème mathématique résolu!).
Résolution sur Inégalités - vous êtes prêt!
10 réflexions sur « Fonctions logarithmiques »
J'ai des problèmes avec faire des transformations mélangées avec des graphiques logarithmiques. L'ordre habituel ne semble pas donner la bonne réponse (retournement 1er, étirement / contraction, puis décalage dernier). Dans l'exemple de ma prof, g (x) = ln (1-x), il est passé en premier, puis réfléchie. Cela déplace la asymptote verticale à x = 1 au lieu de x = -2 (qui est ce qu'elle est si vous reflétez 1er puis retournez). Je ne peux pas obtenir une explication de lui, alors maintenant je suis confus.
Désolé, je voulais dire « au lieu de x = -1 » ci-dessus.
Merci pour l'écriture! La façon dont je le fais est de prendre un -1 de la (1-x) pour obtenir ln (- (x-1)), donc nous avions renversons d'abord sur l'axe y, puis déplacer 1 unité vers la droite. Ensuite, l'asymptote serait à x = 1. Mais si vous ne prenez pas le -1, il faut passer d'abord, puis réfléchir. Cela a-t-il du sens? En outre, un graphique sur la calculatrice graphique pour le voir. Lisa
sensationnel. Cela le rend si facile de voir mon erreur. Merci beaucoup!