Histoire des ordinateurs et l'informatique, Calculateurs, les os de Napier (Napier Rods)

Bones de Napier (Napier Rods)

Voyant il n'y a rien qui est si gênant pour la pratique mathématique ... que les multiplications, les divisions, les extractions carrés et un grand nombre de cubes qui, en plus de la dépense fastidieuse de temps sont. sous réserve de nombreuses erreurs glissantes, je commence donc à considérer [comment] Je pourrais supprimer ces obstacles.
Extrait d'une description du Canon merveilleux de logarithmes

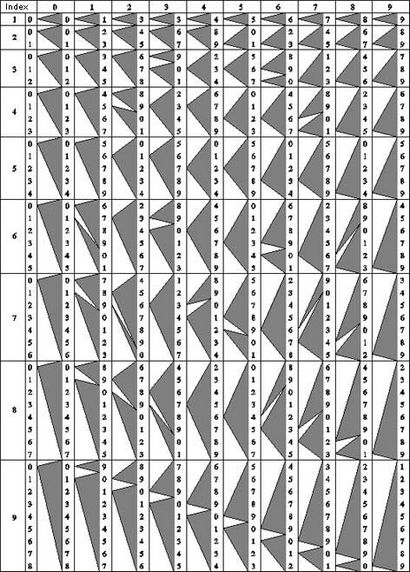
Je n 1617 à Edimbourg après la mort de John Napier (voir biographie de John Napier) a été publié (en langue latine, ce qui était une pratique courante à l'époque) son petit livre -Rabdologiae Seu Numerationis par Virgulas libri duo (voir la photo ci-dessous). Vous cherchez à soulager ses propres difficultés dans le calcul des tables logarithmiques, et impatient avec le processus fastidieux et sujet aux erreurs de travailler avec un grand nombre, Napier a inventé plusieurs méthodes mécaniques de simplifier et d'accélérer la multiplication, les plus célèbres étant des tiges spéciales, plus tard connu comme Napier des os. Outre les virgulas ou tiges, John Napier a décrit multiplicationes promptuario ou promptuary de la multiplication et la Abaco de scacchiae ou Abacus chessboard.

Napier apparemment basé son invention sur un populaire dans cette méthode de temps pour la multiplication, décrite dans plusieurs livres-par exemple. dans le livre du célèbre mathématicien italien Luca Paccioli Summa de Arithmetica, Geometrica, Proportioni et Proportionalita (Tout Arithmétique, Géométrie et Proportion), imprimé à Venise en 1494. Cette méthode a été appelée gelosia (jalousie) en italien. Très probablement ces méthodes anciennes pour la multiplication a été inventé par les mathématiciens indiens, puis a été transféré en Chine et par l'intermédiaire d'Arabie Halifat à l'Europe. La méthode de gelosia est la suivante:

Lorsque le second facteur est multidigital, puis les produits intermédiaires doivent être écrites à la main, se déplaçant d'une position vers la gauche, puis les produits intermédiaires doivent être ajoutés (voir le schéma ci-dessous). Après avoir disposé du côté des tiges de multiplicande à côte, il faut multiplier le multiplicande (46785399) par les unités du multiplicateur (96431). Ce résultat est 46785399x1 = 46785399. Ensuite, il faut multiplier le multiplicande par dizaines multiplicateur 46785399x3 = 140356197, décalant le résultat d'une position à gauche et de continuer, alors que tous les chiffres du multiplicateur seront utilisés. Ensuite, nous devons ajouter manuellement les facteurs partiels. Il était une question de temps, quelqu'un à penser, que si nous avons une machine à additionner, la multiplication peut être fait sans penser, et cela est arrivé seulement quelques années plus tard, Wilhelm Schickard. qui a utilisé les tiges de Napier dans son Rechenuhr (Calcul de l'horloge).

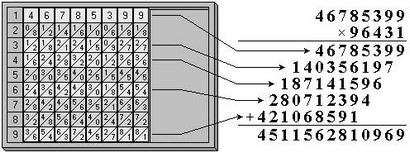
La multiplication des numéros multidigital

carré de gauche est inscrite avec des lettres pour la tige épaisse. Le carré du milieu est inscrit avec des lettres pour la tige pour 6. carré droite est pour les lettres de la tige mince.

Au cours de la multiplication de la tige épaisse est appuyé contre la tige mince de telle manière, que les diagonales des deux grands carrés pour coïncider (barres minces sont mis en rotation à 90 degrés). Puis, dans les ouvertures de la tige mince on peut voir les chiffres du produit des nombres, qui sont inscrits sur ces tiges. Dans la figure suivante, vous pouvez voir la multiplication de 7213x524. doit d'abord être disposés correctement tiges épaisses, selon le multiplicande 7213. Ensuite, les tiges minces, selon le multiplicateur 524, sont placés sur et mis en rotation à 90 degrés par rapport à l'épaisseur, comme les diagonales des carrés sur les tiges épaisses et minces à être simultanée. Le résultat peut être représenté par l'addition de chiffres visibles (dans la figure, les chiffres sont présentés dans les triangles épaissir).

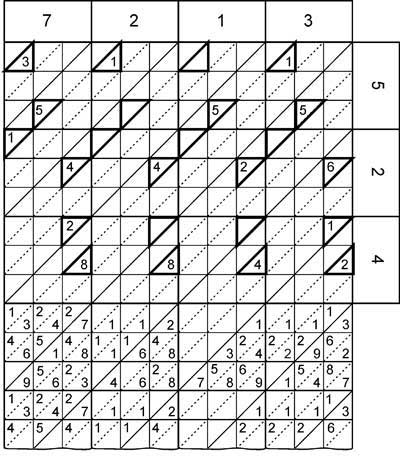
Multiplication 7213x524 avec des tiges promptuary

Dans la description de la promptuary Napier spécifié, qu'il peut être utilisé pour la division aussi. Pour cette action, il suggère à trouver d'abord l'inverse d'un des multiplicateurs, puis à faire une multiplication avec le promptuary.

Au cours des prochains siècles beaucoup d'inventeurs a essayé d'améliorer et de faciliter le travail avec les tiges de Napier, en commençant par le Wilhelm mentionné ci-dessus Schickard au début des années 1620.

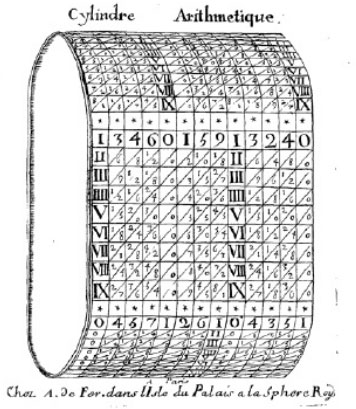
Le cylindre de Pierre Petit Arithmétique

Selon Petit, les gens ont cessé d'utiliser « belle invention » parce que « la multitude et l'embarras de ces bâtons, rempli de chiffres sur tous les côtés, se sont avérés prolongés et fastidieux. » Napier Depuis Petit a trouvé cette méthode de calcul encore utile, et parce qu'il était « plus facile d'améliorer les inventions que de devenir un inventeur », il a conçu de longues bandes ou des rubans de papier contenant chacun tous les multiples de la Rhabdologie de Napier. Ces longues bandes ont ensuite été extrémité fixée à la fin et monté sur un cylindre en bois de la taille du tambour ou un chapeau d'un enfant et d'une longueur qui dépend de la quantité de bandes on voulait avoir pour faire des calculs avec un grand nombre.

Schott non seulement décrit Organum Mathematicum Kircher. mais il a ajouté sa propre amélioration aux barres de navigation à l'estime de Napier (il très probablement ne savait pas pour le Rechenuhr de Schickard. créé au début des années 1620, qui a également utilisé des tiges, des endroits sur la surface d'un cylindre). Au lieu d'avoir à traiter avec un certain nombre de petites tiges individuelles chaque fois que l'on souhaite effectuer la multiplication, Schott a conçu une boîte (cistula) dans laquelle les tiges de Napier ont été convertis en cylindres, chacun d'entre eux incorporant l'ensemble complet des multiples de un à neuf précédemment trouvé sur plusieurs tiges séparées. Pour faire fonctionner la machine, on ne devait tourner les poignées des cylindres à la figure appropriée devait être multipliée, et alors seulement est devenu une question de suivre les règles bien définies de Rhabdologie de Napier. De plus, pour assurer la machine serait utilisée par le plus grand nombre possible de personnes, une table d'addition et de soustraction a été fournie sur la couverture intérieure de la boîte.

Plus tard l'outil de multiplication de Organum mathematicum (avec une amélioration de Schott) a été décrit dans Theatrum arithmético- geometricum de Leupold. L'outil arithmétique se compose de dix cylindres, sur lequel sont placées des bandes surface avec des tiges de Napier inscrits. Les cylindres (voir la figure du bas) sont montés dans une boîte, qui est fermé à la face supérieure d'une feuille de carton doublé avec des fentes verticales étroites. Du côté avant de la boîte sont placés poignées fixées aux cylindres, qui peuvent être utilisés pour faire tourner des cylindres, peut être ainsi réglé multiplicande nécessaire sur les tiges. Sur le côté intérieur du couvercle articulé de la boîte est inscrite une table d'addition pour aider l'opérateur.

L'outil arithmétique des Organum Mathematicum dans Theatrum arithmético-geometricum de Leupold

Dans le arithmético- geometricum Theatrum de Leupold, déjà mentionné dans cet article, est décrit également un outil de calcul, ainsi appelé calcul de tambour. sur la base des tiges de Napier (voir la figure du bas). Examinons sa construction.

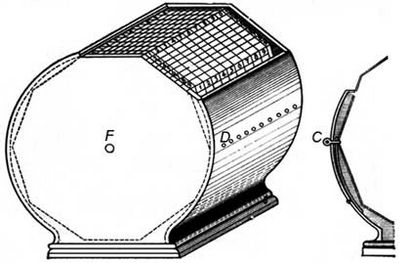
Dispositif de tiges de Napier Leupold (tambour de calcul)

En 1789, le mathématicien allemand M. Prahl a conçu un instrument, qu'il appelait Arithmetica Portatilis. et qui était le même que le Pythagorica Mensula de Poetius, à l'exception seulement que les cercles mobiles étaient beaucoup plus grandes et porté les numéros 1 à 100, de telle sorte que, à l'aide de l'instrument que le nombre pourrait être ajouté et soustrait à 100.