La demi-vie et désintégration radioactive Kinetics
Ce livre est distribué sous licence une licence Creative Commons by-nc-sa 3.0. Voir la licence pour plus de détails, mais cela signifie, fondamentalement, vous pouvez partager ce livre aussi longtemps que vous citez l'auteur (mais voir ci-dessous), ne font pas d'argent de lui, et ne le rendre accessible à tout le monde dans les mêmes termes.
copies PDF de ce livre ont été générés à l'aide du Prince. un excellent outil pour faire des fichiers PDF en HTML et CSS. Plus de détails sur le processus sont disponibles dans ce billet de blog.
Est-ce que ce livre vous a aidé? Pensez à passer sur:
Creative Commons soutient la culture libre de la musique à l'éducation. Leurs licences ont contribué à faire ce livre à votre disposition.
DonorsChoose.org aide les gens comme vous aider les enseignants à financer leurs projets de classe, de fournitures d'art aux livres à des calculatrices.
Section précédente
Table des matières
Section suivante
Objectif d'apprentissage
- Pour savoir comment utiliser des demi-vies pour décrire les taux de réactions de premier ordre.
Les demi-vies
La demi-vie d'une réaction de premier ordre dans un ensemble donné de conditions de réaction est une constante. Ce n'est pas vrai pour les réactions zeroth- et de second ordre. La demi-vie d'une réaction du premier ordre est indépendant de la concentration des réactifs. Cela devient évident quand nous réorganisons la loi de vitesse intégré pour une réaction de premier ordre (équation 14.21) pour produire l'équation suivante:
Substituant [A] 0/2 [A] et t1 / 2 pour t (pour indiquer une demi-vie) dans l'équation donne 14,27
Ainsi, pour une réaction de premier ordre, chaque demi-vie successive est la même longueur de temps, comme le montre la figure 14.17 « La demi-vie d'une réaction de premier ordre ». et est indépendante de [A].
Figure 14.17 La demi-vie d'une réaction de premier ordre
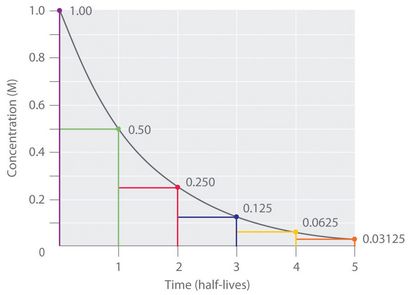
Si nous savons que la constante de vitesse pour une réaction de premier ordre, nous pouvons utiliser des demi-vies pour prédire combien de temps est nécessaire pour la réaction d'atteindre un certain achèvement pour cent.
Nombre de demi-vies
Comme vous pouvez le voir sur ce tableau, la quantité de réactif gauche après n demi-vie d'une réaction de premier ordre est (1/2) n fois la concentration initiale.
Notez le motif
exemple 10
Compte tenu: constante de vitesse, la concentration initiale et le nombre de demi-vie
Demandées: demi-vie, les concentrations finales, et pour cent achèvement
Une utilisation équation 14,28 pour calculer la demi-vie de la réaction.
B Multiplier la concentration initiale de 1/2 à la puissance correspondant au nombre de demi-vies pour obtenir les concentrations restantes après les demi-vies.
C Soustraire la concentration restante de la concentration initiale. Puis diviser par la concentration initiale, en multipliant la fraction de 100 pour cent pour obtenir l'achèvement.
A Nous pouvons calculer la demi-vie de la réaction en utilisant l'équation 14,28:
Ainsi, il prend presque 8 h pour la moitié du cisplatine à hydrolyser.
B Après 5 demi-vies (environ 38 h), la concentration restante de cisplatine sera comme suit:
Au bout de 10 demi-vie (77 h), la concentration restante de cisplatine sera comme suit:
C L'achèvement de 5 pour cent après la demi-vie sera comme suit:
L'achèvement de 10 pour cent après la demi-vie sera comme suit:
Ainsi, une réaction chimique de premier ordre est de 97% après 5 demi-vies et 100% après 10 demi-vies.
L'activité est généralement mesurée en désintégrations par seconde (dps) ou désintégrations par minute (dpm).
L'activité d'un échantillon est directement proportionnelle au nombre d'atomes de l'isotope radioactif dans l'échantillon:
Tableau 14.6 demi-vies et applications de certains isotopes radioactifs
Techniques Rencontres radioisotopes
Figure 14.18 radiocarbone Dating
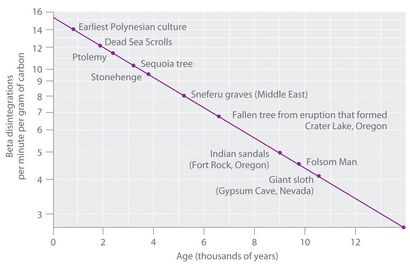
Un tracé de l'activité spécifique de 14 C par rapport à l'âge pour un certain nombre d'échantillons archéologiques montre une relation linéaire inverse entre la teneur en 14 C (une échelle logarithmique) et l'âge (échelle linéaire).
exemple 11
Étant donné: isotope et l'activité finale
Nous avons demandé: temps écoulé
Une utilisation équation 14,30 pour calculer N0 / N. remplacer la valeur de la demi-vie de 14 C dans l'équation 14,28 pour trouver la constante de vitesse pour la réaction.
B En utilisant les valeurs obtenues pour N0 / N et la constante de vitesse, résoudre l'équation 14,32 pour obtenir le temps écoulé.
A partir de l'équation 14.30. nous savons que A = kN. On peut donc utiliser les activités initiales et finales (A0 = dpm 15 et A = 8,0 dpm) pour calculer N0 / N:
A 0 A = k 0 k N N = N N = 0 15 8,0
Maintenant, il faut calculer que la constante de vitesse pour la réaction de sa demi-vie (5730 ans) en utilisant l'équation 14,28:
Cette équation peut être réorganisée comme suit:
B substituant dans l'équation de t,
De nos calculs, l'homme est mort il y a 5200 ans.
points clés
- La demi-vie d'une réaction du premier ordre est indépendant de la concentration des réactifs.
- La demi-vie des isotopes radioactifs peuvent être utilisés pour des objets de date.
Les équations clés
La demi-vie de la réaction du premier ordre