Let - s Tackle un classique, physique Wicked problème

Voici problème de la physique classique (et difficile) qui pose une question intéressante:

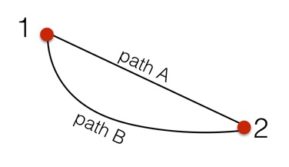
Prenez deux points dans l'espace, les points 1 et 2. Quel est le chemin du point de 1 à 2 qu'un objet peut glisser dans frottement le moins de temps? Supposons un champ gravitationnel constant.

Voici deux points avec des chemins différents. On pourrait être plus rapide, mais qui serait le plus rapide? La solution à ce problème est traditionnellement appelé la courbe de brachistochrone.

Cette question difficile et intéressante a une signification historique. La solution brachistochrone a contribué à la création du calcul des variations. J'ai gagné # x27; t aller dans les détails, mais je vous rappelle que la mécanique est Lagrangiennes basée sur le calcul des variations.

L'approche traditionnelle des manuels scolaires est ici pour résoudre d'abord le temps de glisser vers le bas une courbe. Depuis une courbe ISN # x27; t droite, vous devez définir cela comme une intégrale dans laquelle vous calculez le temps nécessaire pour de nombreux petits segments « droites » et les ajouter. Ce # x27; est pas trop difficile. La partie la plus délicate est de trouver la fonction (courbe) qui donne la valeur minimum après l'intégration. Il # x27; s comme un problème max-min en calcul mais beaucoup plus difficile.

I # x27; ai passé sur la dérivation du calcul des variations quand j'enseigne la mécanique classique, mais je # x27; ai jamais été satisfait. Je me sens toujours # x27, de la sorte d'une étape magique et mystérieuse de trouver cette fonction qui minimise l'intégrale, et je suis juste avec le livre un peu comme je viens de suivre mon téléphone # x27, les instructions s en essayant de trouver une nouvelle emplacement.

Mais avec un grand problème, il y a plus d'une façon de résoudre ce problème. Qu'en est-il un certain type de solution numérique? Oui, ce # x27; s ce que je # x27; ferons au moins pour l'une des solutions.

Intuition humaine

J'ai une idée pour un jeu. Un jeu de physique avec des problèmes compliqués. L'utilisateur (joueur) tente de deviner des solutions sans résoudre réellement les problèmes. Bien sûr, ces jeux exis- déjà beaucoup de basket-ball et le baseball avec le mouvement du projectile, même si personne ne résout en fait pour ces trajectoires. Mais qu'en est-deviner les niveaux d'énergie pour un objet quantique? Ou la vitesse pour une orbite planétaire stable? Cela pourrait être un jeu amusant.

Mais voici un exemple concret: Pouvez-vous estimer le chemin qui permettrait une lame de talon vers le bas un fil dans les plus brefs délais? Eh bien, je mets ensemble un code python qui laisse # x27; s vous testez votre intuition. Voici # x27; s comment jouer:

• Ajustez les boules grises pour changer le chemin de la courbe du point 1 au point 2. Astuce: vous pouvez cliquer et faire glisser dans un chemin et il devrait déplacer les points que vous passez sur eux.
• Cliquez sur « Exécuter » et regarder la lame de talon. La minuterie révélera le temps de diapositive totale.
• Vous pouvez essayer à nouveau. Cliquez simplement sur « pause » et « reset » et vous devriez être bon d'aller.

Voici le programme.

Si vous voulez vraiment regarder le code, ici il est. I # x27; ll être honnête, je ne çA x27, comprends complètement les boutons ou les interactions de la souris, mais je l'ai eu à travailler.

Solution numérique

La clé d'une solution numérique est de prendre un problème complexe et le casser en un tas de problèmes plus simples. Et s'il y avait juste un point mobile entre deux points fixes?

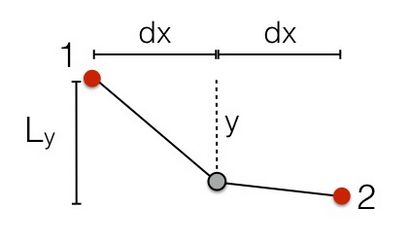
Ici, je peux déplacer la position centrale de haut en bas (avec une variable y) et calculer le temps qu'il faut pour aller de la position 1 à 2. Permettez-moi un peu différent ce que le problème d'origine. Dans ce cas, je vais laisser la perle commence à la position 1 avec une vitesse de départ. Le bourrelet accélère lorsqu'il se déplace vers le point milieu (en supposant que je le déplacer plus bas que le point de départ).

Calcul du temps pour atteindre le point médian ISN # x27; t difficile, mais il est un peu fastidieux. Tout d'abord, je vais calculer la vitesse de la bille au milieu. Ici, je peux utiliser le principe de travail d'énergie. En utilisant l'énergie potentielle gravitationnelle et un changement d'énergie cinétique, je reçois:

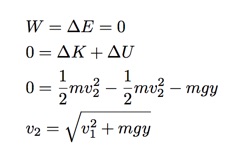
Pour le temps de Voyage, j'ai besoin de la vitesse moyenne et la distance. La vitesse moyenne est la somme de la vitesse de début et de fin divisée par deux (puisque l'accélération est constante). Je vais appeler la distance pour ce chemin partiel la variable s. Il aura la valeur suivante.

Peut-être vous avez remarqué que je fais appel « vers le bas » la direction y positive. J'espère que didn # x27; mess t vous vers le haut. Maintenant, je peux mettre la vitesse moyenne en même temps que la distance pour obtenir le temps de diapositive. Rappelez-vous le talon doit rester sur le fil afin # x27; s un problème de dimension.

Oui, à la fois v 2 et s dépendent de la Position- verticale y. Mais attendez! Nous aren encore # x27; t fini. Maintenant, je dois faire la même chose pour le chemin du milieu au point 2. Rappelez-vous deux choses importantes. Tout d'abord, la vitesse finale de la première partie est la vitesse de départ de la seconde partie. En second lieu, il # x27; est très possible que l'accélération de la perle est négative (si le fil monte).

Cependant, le point est qu'il # x27, tout à fait possible obtenir une expression de la perle temps en fonction de la variable y. Avec cette expression, ces choses pourraient se transformer en un problème max-min classique. Cela pourrait se faire, mais il obtiendrait en désordre. Ainsi, au lieu, je # x27; vais faire autre chose.

Que faire si je viens de mettre le point milieu à une valeur de y et calculer le temps total. Ensuite, je vais déplacer la position y et calculer le temps total à nouveau. Avec cela, je pourrais faire un terrain de glissement du temps par rapport à la position y. Il serait si simple que je pouvais le faire en ce moment.

Maintenant, pour mettre ce calcul à quelque chose de plus utile. J'ai juste besoin d'exécuter le même calcul pour chaque point dans ma courbe. Oui, cela peut être lent, mais il fonctionne. Ici # x27; s ce qui ressemble. Cliquez sur « play » pour démarrer.

Je pense que # x27; est assez impressionnant. Honnêtement, cela m'a pris un peu plus de temps à mettre en place que prévu. En fin de compte, il semble assez agréable. Oh, vous le dites # x27; est pas la solution la plus rapide? Eh bien, avez-vous déjà essayé de résoudre ce problème sur le papier? Il # x27, est assez difficile.

Calcul des variations

Mais comment ma solution à comparer la réponse de manuel traditionnel? Soit dit en passant, si vous voulez aller sur la dérivation, je suggère à la recherche à Andy Rundquist # x27; s après sur ce point.

J'ai gagné # x27; t couvrir les détails de la solution, sauf pour dire que le chemin le plus court chronométré est celui d'une cycloïde. Mais je suis surpris que ce n'était pas # x27; t si trivial de trouver un chemin cycloïde qui a commencé et a pris fin aux points de droit. Je devais faire un autre calcul numérique pour trouver l'un des coefficients mais j'ai gagné # x27; t aller dans cela.

En fin de compte, j'ai pu modifier mon programme pour inclure une cycloïde avec mon optimisation numérique. Ici, il est presse jeu pour l'exécuter. La courbe jaune est la solution analytique.

Je # x27; suis très heureux.

Don # x27; oubliez vos devoirs.

Mise à jour (16/01/17). Dans une conversation par courriel avec Bruce Sherwood, je me suis souvenu d'un vieux (mais célèbre) programme de physique appelé les graphiques et les pistes. L'idée de base de ce programme était un étudiant d'ajuster une piste qu'une balle pourrait rouler sur de telle sorte que le graphique de la position, la vitesse, l'accélération correspond une idée prédéfinie. Il était assez impressionnant et assez semblable au code que je produis ci-dessus.

• 

Netflix # x27; arme secrète de Isn # de x27; t Redémarre-It # x27; Films Genre de

Lyft dit: « Moi aussi! » Et plonge dans le jeu auto-conduite

New Comms Trump Directeur Hates La plupart d'entre Trump # x27; s politiques

Emma Gray Ellis

So Long, Spicey. Merci pour tous les mèmes

Comment Faux Cops Got 1,2 million $ en armes réelles