Physique Rocket de l'eau
fusées d'eau sont des jouets amusants pour les personnes de tous âges, même les adultes. Ils travaillent sur la base d'un concept simple de la physique dans lequel l'eau est forcé le fond de la fusée par la pression de l'air, et ce faisant exerce alors une force ascendante poussant vers le haut sur la fusée (troisième loi de Newton). Cette force vers le haut provoque la fusée pour tirer vers le haut à grande vitesse. La façon dont fonctionne une fusée à eau est en le remplissant partiellement à l'eau puis mise sous pression à l'intérieur avec de l'air. Lorsque l'embout inférieur est ouvert, les forces de pression d'air interne de l'eau hors de cette buse à grande vitesse provoquant la fusée pour tirer vers le haut à grande vitesse.
Les amateurs de fusées à eau ont créé toutes sortes de modèles de fusées d'eau incroyables, dont celui-ci montre la vidéo ci-dessous qui est une fusée à eau à deux étages.
Ensuite, je vais entrer dans une partie de la physique des fusées à eau. L'analyse sera un peu avancé, mais il est un moyen pour une fin dans laquelle le résultat final vous aidera à construire et mettre en place une fusée d'eau qui atteindra une hauteur maximale dans l'air.
Analyse de la physique Rocket de l'eau
La figure ci-dessous montre un schéma pour cette analyse.
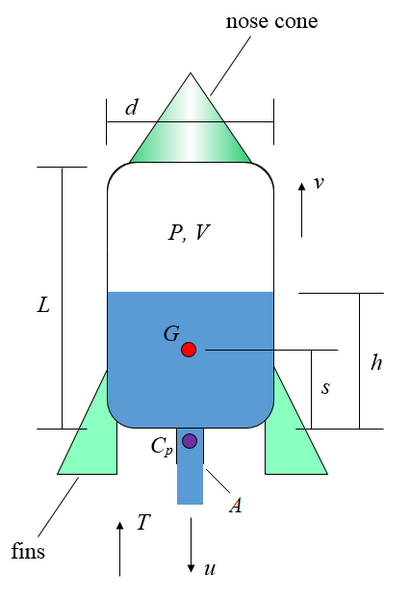
d est le diamètre du corps de fusée
L est la longueur du corps de fusée
P est la pression d'air à l'intérieur du corps de fusée
V est le volume d'air à l'intérieur du corps de fusée
G est le centre de masse du système de fusée + eau (où l'eau est celle qui est contenue à l'intérieur du corps de fusée). Notez que la masse de l'air à l'intérieur de la fusée est assez petit pour être ignoré
Cp est le centre de pression (de la force de traînée de l'air) pour la fusée lorsqu'il est en vol
A est la surface en coupe transversale de la tuyère de la fusée (par laquelle les sorties d'eau)
u est la vitesse de l'eau sortant par rapport à la fusée
T est la poussée exercée sur la fusée, créée par l'eau sortant
s est la distance entre le fond du corps de fusée par rapport au centre de masse G
h est la hauteur de l'eau, comme le montre
v est la vitesse de la fusée, par rapport à la masse
Le cône de nez (représenté sur la figure ci-dessus) permet de réduire la résistance à l'air que la fusée vole dans les airs. Notez également que nous partons du principe d'un corps de fusée à paroi mince dans laquelle les dimensions d. L. h. et s sont approximativement les mêmes (avec une différence négligeable) soit mesurée à partir des surfaces intérieures du corps de fusée ou des surfaces extérieures du corps de fusée.
Lorsque la vitesse augmente fusée elle rencontre la résistance de l'air (traînée) qui peut provoquer la fusée d'extrémité sèche sur l'extrémité. Pour éviter ce ailettes doit être placé sur la fusée (représentée sur la figure ci-dessus) qui provoquent la force de traînée résultant de la résistance à l'air d'agir en un point situé au-dessous de G. connu sous le centre de pression Cp. Cela permettra à la force de traînée pour maintenir la fusée aligné sur sa trajectoire de vol et tumbling ne se produira pas. Les ailettes doivent être situés assez bas sur le corps de fusée de sorte que le centre de pression Cp est toujours inférieure à G (dont la position change à mesure que la sortie de l'eau). Cela garantira que la fusée ne sera jamais sèche à tout moment au cours de son vol, et il sera donc stable car il vole dans les airs. Le commerce hors de placer des ailettes est qu'ils sont une source de résistance à l'air et provoquent force de traînée supplémentaire sur la fusée en raison, mais sans eux la fusée serait sèche car il vole dans les airs et ne pas aller très élevé en conséquence.
Nous allons maintenant développer les équations pour modéliser le vol d'une fusée d'eau.
Le T de poussée pour une fusée d'eau est le même que pour les fusées chimiques décrites dans la page de la physique des fusées. La poussée est donnée par:
où m est la masse de la fusée d'eau (corps de fusée + eau), et t est le temps.
On peut raisonnablement supposer que, lorsque l'eau est sortie, le volume d'air à l'intérieur du corps de fusée se développe assez rapidement, de sorte qu'il n'a pas le temps de faire l'expérience soit le gain de chaleur de l'environnement extérieur ou la perte de chaleur à l'environnement extérieur. En thermodynamique ce qu'on appelle une détente adiabatique (ou un processus isentropique), et elle peut être représentée mathématiquement par l'équation suivante:
C est une constante
k est une constante thermodynamique, qui pour l'air est égale à 1,4
Po est la pression absolue initiale de l'air à l'intérieur du corps de la fusée, avant que l'eau est libérée
Vo est le volume initial de l'air à l'intérieur du corps de la fusée, avant que l'eau est libérée
De l'équation de Bernoulli pour l'écoulement de fluide de densité constante,
Pa est la pression d'air à l'extérieur du corps de fusée. Ceci est supposé constant sur la distance de vol de la fusée
ρ est la masse volumique de l'eau, qui est de 1000 kg / m 3
Cette équation suppose ce qui suit:
- La vitesse d'écoulement de l'eau à l'interface air-eau à l'intérieur du corps de fusée est négligeable par rapport à la vitesse d'écoulement de sortie u. Notez que la vitesse d'écoulement est la vitesse par rapport à la fusée.
- Le changement dans l'énergie gravitationnelle de l'eau comme il change d'élévation en coulant à l'intérieur du corps de fusée à l'extérieur a une contribution négligeable.
- des conditions d'écoulement quasi-stationnaire pour l'eau, avec un frottement négligeable de fluide.
D'après l'équation (1)
Remplacer cette équation dans l'équation (3) et nous obtenons
T résolvons et nous obtenons
Substitut équation (2) dans l'équation (3). Cela nous donne
Nous cherchons maintenant une équation dans laquelle u peut être calculé en fonction du temps. Cela permettra alors une poussée T à donner en fonction du temps. équation différencier (7) par rapport au temps. Cela nous donne
où dV / dt est le taux de variation du débit d'air à l'intérieur du corps de fusée. Ceci est égal au débit de volume d'eau sortant du corps de fusée. Donc,
Substituer cette équation dans l'équation (8). On a
Substitut de V à partir de l'équation (7) dans l'équation ci-dessus et de simplifier. Cela nous donne
D'après l'équation (5),
On peut remplacer u calculée à partir de l'équation (10) dans cette équation pour obtenir T en fonction du temps.
Un problème intéressant et pratique est de déterminer la hauteur maximale atteinte par une fusée d'eau, en tenant compte de la résistance à l'air. Par la deuxième loi de Newton le (unidimensionnelle) l'équilibre de force pour la fusée de l'eau est
où g est l'accélération due à la pesanteur (9,8 m / s 2) et D est la force de traînée due à la résistance de l'air. Ceci est donné par
Cd est le coefficient de traînée
ρa est la masse volumique de l'air
Ac est la surface en coupe transversale du corps de la fusée dans la direction de v
Par conséquent, l'équilibre de force pour la fusée de l'eau devient
L'équation (11) est valable uniquement jusqu'au point la hauteur maximale est atteinte. En effet, (dans cette équation) le terme de traînée ne renverse pas signe pour opposer le mouvement lorsque la vitesse fusée change v signe (et devient négatif) lorsque la fusée tombe après la hauteur du pic est atteint. Pour faire face à la vitesse de la fusée changement de signe après la hauteur du pic est atteint, nous faisons simplement le terme de traînée positif (au lieu de négatif) après la hauteur du pic est atteint, et cela compte bien pour le glisser. Cependant, nous ne devons pas le faire parce que nous ne sommes intéressés à modéliser correctement le vol de la fusée jusqu'au point atteint la hauteur du pic, ce qui nous permet de prédire avec précision la hauteur du pic atteint, ce qui est tout ce que nous préoccupons.
Un beau problème d'optimisation est de déterminer la quantité d'eau à mettre dans le corps de fusée pour obtenir la hauteur maximale, étant donné une pression initiale.
Les équations dérivées ici ont été incorporés dans une feuille de calcul Excel que vous pouvez facilement utiliser pour vous aider à concevoir une fusée d'eau qui atteint la hauteur maximale possible. Pour télécharger la feuille de calcul Excel clic droit sur ce lien. Ce fichier Excel est compressé en format « zip » et vous devez le décompresser avant de pouvoir l'utiliser.
Remplissage de la fusée avec de l'air sous pression ne sera pas entraîner presque aussi grande hauteur atteint comme vous le feriez en remplissant la fusée avec de l'air sous pression et de l'eau. En effet, l'air d'échappement dans la fusée d'air uniquement (après avoir été libéré) obtient une plus grande part de l'énergie stockée (de la pression initiale) que l'eau serait échapper dans une fusée à eau. Cela est dû à la masse beaucoup plus d'eau que l'air, à l'intérieur de la fusée. Ce processus est analogue à tirer une balle de fusil. La balle, ayant beaucoup moins de masse que l'arme à feu, obtient une part beaucoup plus importante de l'énergie de la poudre à canon que l'arme à feu. Si vous voulez l'arme d'avoir une plus grande part de l'énergie (et donc une plus grande vitesse de recul après le tir), la balle doit avoir plus de masse. Par analogie, la balle représente le contenu de la fusée (soit de l'air seul ou eau + air), et le canon représente le corps de fusée. Étant donné que l'eau a une masse beaucoup plus grande que l'air (intérieur de la fusée), le résultat est que le corps de fusée obtiendra une part beaucoup plus grande de l'énergie stockée. Cela se traduit par une plus grande énergie cinétique de la fusée (et donc beaucoup plus grande vitesse) d'une fusée d'air seule, ce qui se traduira par elle atteignant une hauteur beaucoup plus grande que d'une fusée d'air uniquement. Pour voir une démonstration détaillée de ce concept, voir la différence entre l'élan et l'énergie cinétique.
Idéalement, la fusée est mise sous pression de sorte que, comme le dernier des sorties d'eau, la pression à l'intérieur de la fusée est à la pression atmosphérique. Cela représente la conception la plus efficace, même si elle se traduira pas nécessairement la plus grande hauteur atteint pour une pression initiale donnée. Si la pression d'air à l'intérieur de la fusée est supérieure à la pression atmosphérique, comme le dernier des sorties de l'eau, l'air de tirer bien sûr le fond et une poussée supplémentaire (et la vitesse) sera donnée à la fusée. Cependant, ce n'est pas comptabilisé ici, étant donné que sa contribution à la hauteur maximale atteinte est presque négligeable, pour les raisons indiquées au paragraphe précédent.
remplir complètement la fusée d'eau avec de l'eau va l'empêcher d'être sous pression puisque l'eau est incompressible pour les pressions typiques utilisées dans les fusées d'eau.
Si la masse du corps de fusée (eau exclue) est trop faible, la force de traînée sera trop élevé par rapport à la force de gravité, pendant la partie de la phase de vol où il n'y a pas de poussée. En conséquence, la hauteur atteinte par la fusée sera effectivement moins que pour un corps de fusée plus lourd. Par analogie, si vous lancez une boule de mousse de polystyrène et une boule de métal de la même taille droite en l'air, à la fois avec la même énergie cinétique initiale, la boule de métal atteindra une hauteur plus élevée, même si la boule de styromousse doit être lancé avec beaucoup plus grande vitesse afin d'avoir la même énergie cinétique que la bille métallique (en raison de sa masse beaucoup plus faible).
La phase de poussée de l'eau typique pour une fusée de taille de la bouteille est très courte, qui dure généralement un dixième de seconde environ. Ceci est combien de temps il faut pour toute l'eau pour sortir de la fusée. Au cours de cette période la fusée accélère très rapidement.
Retour de la physique Rocket de l'eau à la page Divers Physique
Retour de la physique Rocket de l'eau à la physique problèmes réels page d'accueil