Règles de probabilité pour héritage mendélienne
Objectif d'apprentissage
Calculer la probabilité de traits de plantes de pois en utilisant des croix mendélienne
Points clés
- La règle de produit est utilisé pour déterminer le résultat d'un événement avec deux événements indépendants; la probabilité de l'événement est le produit des probabilités de chaque événement individuel.
- La somme règle est utilisée pour déterminer le résultat d'un événement avec deux événements mutuellement exclusifs de multiples voies; la probabilité de l'événement est la somme des probabilités de chaque cas individuel.
- La règle du produit de la probabilité est utilisée pour déterminer la probabilité d'avoir les deux traits dominants de la descendance F2; il est le produit des probabilités d'avoir le trait dominant pour chaque caractéristique.
- La somme règle de probabilité est utilisée pour déterminer la probabilité d'avoir un trait dominant dans la génération F2 d'un croisement dihybride; il est la somme des probabilités de chaque individu avec ce trait.
un nombre entre 0 et 1, exprimant la probabilité précise d'un événement qui se passe
la probabilité de deux événements indépendants se produisent en même temps peut être calculée en multipliant les probabilités individuelles de chaque événement se produisant seul
la probabilité de la survenance d'un événement ou l'autre cas, de deux événements mutuellement exclusifs, est la somme de leurs probabilités individuelles
Principes de base de probabilité
Probabilités sont des mesures mathématiques de probabilité. La probabilité empirique d'un événement est calculé en divisant le nombre de fois où l'événement se produit par le nombre total d'opportunités pour l'événement de se produire. probabilités empiriques proviennent d'observations telles que celles de Mendel. Un exemple d'un événement génétique est une graine ronde produite par une plante de pois. Mendel a démontré que la probabilité de l'événement « graine ronde » pas de se produire chez les descendants F1 des parents vrais élevage, dont un a des graines rondes et dont l'une a graines ridée. Lorsque les plantes F1 ont ensuite été auto-croisés, la probabilité que les enfants nés F2 donné ayant des graines rondes était trois sur quatre. En d'autres termes, dans une large population de descendance F2 choisi au hasard, 75 pour cent étaient censés avoir le tour des graines, alors que 25 pour cent étaient censés avoir des graines ridées. En utilisant un grand nombre de croix, Mendel a pu calculer les probabilités et les utiliser pour prédire les résultats d'autres croisements.
La règle du produit
Mendel a démontré que les caractéristiques de plantes de pois, il a étudié ont été transmis sous forme d'unités discrètes des parents aux descendants. Mendel a également déterminé que des caractéristiques différentes ont été transmises indépendamment les uns des autres et pourraient être pris en compte dans l'analyse probabilité séparée. Par exemple, d'effectuer un croisement entre une plante à graines vertes, ridé et une plante de jaune, graines rondes progéniture produite qui avait un rapport de 3: 1 de vert: graines jaunes et un rapport 3: 1 de ronds: graines ridée. Les caractéristiques de couleur et de texture n'a pas influencé l'autre.
Parmi les 12 résultats possibles, la filière a une 12/02 (ou 06/01) probabilité d'obtenir un deux, et le denier a un 12/06 (ou 02/01) probabilité de venir têtes. La probabilité que vous obtenir les résultats combinés 2 et la tête est la suivante: (D2) x (PH) = (1/6) x (1/2) ou 1/12. Le mot « et » est un signal d'appliquer la règle du produit. Voyez comment la règle du produit est appliqué à un dihybride. la probabilité d'avoir les deux traits dominants dans la descendance F2 est le produit des probabilités d'avoir le trait dominant pour chaque caractéristique.
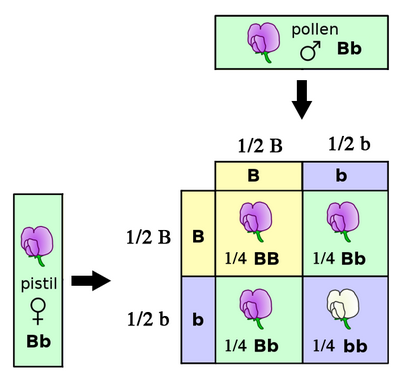
De la probabilité dans la ségrégation des allèles et la fertilisation
Dans un croisement génétique, la probabilité que le trait dominant étant exprimé dépend de sa fréquence. Dans ce cas, les deux parents possédaient une dominante et un gène récessif pour le trait de la couleur des fleurs. Le trait dominant est exprimé en 3/4 de la progéniture et le trait récessif est exprimé en 1/4.
La règle Somme
La règle de la somme est appliquée lorsque l'on considère deux résultats mutuellement exclusifs qui peuvent résulter de plus d'une voie. Il indique que la probabilité de la survenance d'un événement ou d'une autre, de deux événements mutuellement exclusifs, est la somme de leurs probabilités individuelles. Le mot « ou » indique que vous devez appliquer la règle de somme. Imaginons que vous êtes en feuilletant un sou (P) et un quart (Q). Quelle est la probabilité d'une pièce à venir têtes et une queue à venir? Ceci peut être réalisé par deux cas: le penny est la tête (PH) et le quartier est queue (QT), ou le trimestre est la tête (QH) et le denier est queue (PT). Les deux cas satisfait du résultat. On calcule la probabilité d'obtenir une tête et une queue en tant que [(PH) × (QT)] + [(QH) x (PT)] = [(1/2) x (1/2)] + [(1 / 2) x (1/2)] = 1/2. Vous devriez également remarquer que nous avons utilisé la règle du produit pour calculer la probabilité de PH et QT ainsi que la probabilité de PT et QH. avant de les additionnées. La règle de la somme peut être appliquée pour montrer la probabilité d'avoir un seul trait dominant dans la génération F2 d'un croisement de dihybride.
Pour utiliser les lois de probabilité dans la pratique, il est nécessaire de travailler avec les grandes tailles d'échantillons, car la petite taille de l'échantillon sont sujettes à des écarts causés par hasard. Les grandes quantités de plants de pois que Mendel lui ont permis de examiné calculer les probabilités des traits qui apparaissent dans sa génération F2. Cette découverte signifie que lorsque les traits parentaux étaient connus, les traits de la progéniture pouvait prévoir avec précision, même avant la fécondation.