Triangle Problèmes similaires

Précédent ◈ Suivant

Problème 1: Dans le triangle ABC représenté ci-dessous, A'C » est parallèle à courant alternatif. Trouvez la longueur y de la Colombie-Britannique » et la longueur x de A'A.

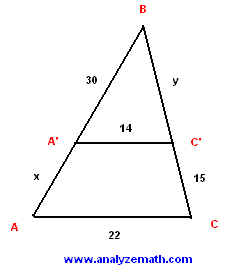
Solution au problème 1:

BA est une coupe transversale que les deux lignes parallèles A'C « et AC, donc les angles correspondants BA'C » et BAC sont congruents. BC est également transversal aux deux lignes parallèles A'C « et AC et donc des angles de BC'A » et BCA sont congruents. Ces deux triangles ont deux angles congrus sont donc semblables et les longueurs de leurs côtés sont proportionnels. Séparons les deux triangles comme illustré ci-dessous.

Nous utilisons maintenant la proportionnalité des longueurs du côté d'écrire des équations qui aident à résoudre pour x et y.

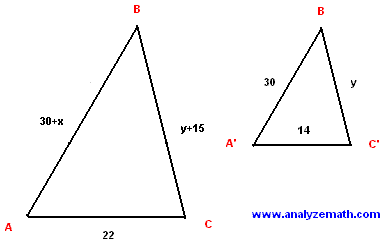
(30 + x) / 30 = 22/14 = (y + 15) / y

(30 + x) / 30 = 22/14

Résoudre le ci-dessus pour x.

22/14 = (y + 15) / y

Résoudre le haut pour y obtenir.

Problème 2: Une équipe de recherche souhaite déterminer l'altitude d'une montagne comme suit: Ils utilisent une source de lumière en L, monté sur une structure de hauteur 2 mètres, pour rayonner un faisceau de lumière à travers le sommet d'un poteau P » par la haut de la montagne M ». La hauteur du mât est de 20 mètres. La distance entre l'altitude de la montagne et le pôle est de 1000 mètres. La distance entre le pôle et le laser est de 10 mètres. Nous partons du principe que la source lumineuse de montage, le pôle et l'altitude de la montagne sont dans le même plan. Trouvez l'altitude h de la montagne.

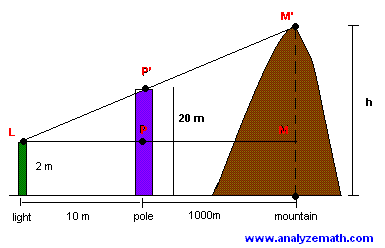
Solution au problème 2:

Nous avons d'abord tracer une ligne horizontale LM. PP « et MM » sont verticales au sol et donc parallèles entre elles. Depuis PP « et MM » sont parallèles, les triangles PPPL « et LMM » sont similaires. D'où la proportionnalité des côtés donne:

1010-1010 = (h - 2) / 18

Pour résoudre h pour obtenir

Problème 3: Les deux triangles sont semblables et le rapport des longueurs de leurs côtés est égale à k: AB / A'B '= BC / B'C' = CA / C'A »= k. Trouver le rapport BH / B'H » des longueurs des courbes des deux triangles.

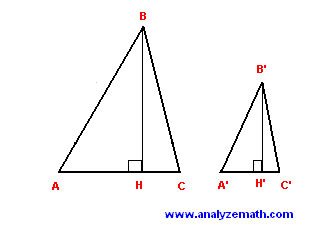
Solution au problème 3:

Si les deux triangles sont semblables, leurs angles correspondants sont congruents. D'où l'angle BAH et B'A'H sont congruents. Nous examinons maintenant la BAH triangles et B'A'H ». Ces triangles ont deux paires d'angles congruents correspondant: BAH et B'A'H « et les triangles rectangles BHA et B'H'A ». Les triangles sont similaires et, par conséquent:

Problème 4: BA « et AB » sont des accords d'un cercle qui se croisent à C. Trouver une relation entre les longueurs des segments AC, BC, B'C et a'c.

Solution au problème 4:

Nous avons d'abord joignons points B et A et B « et A ». Angles ABA « et AB'A » dans les deux triangles sont congruents car ils interceptent le même arc. Angles BAB « et BA'B » intercepter également le même arc et donc en harmonie. Les deux triangles ABC et A'B'C ont deux angles congruents correspondants et sont donc semblables.

Avant d'écrire la proportionnalité des côtés, on sépare d'abord les deux triangles et d'identifier les côtés correspondants puis écrire la proportionnalité des longueurs des côtés.

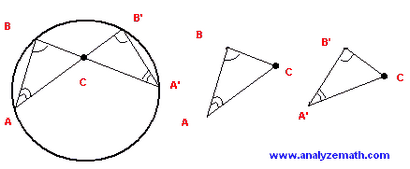
AB / A'B '= BC / B'C = CA / CA'

Puisque nous sommes à la recherche d'une relation entre les longueurs de AC, BC, B'C et A'C, nous utilisons donc la dernière équation et produit croisé pour obtenir

Problème 5: ABC est un triangle. AM est perpendiculaire depuis le sommet A de l'hypoténuse BC du triangle. Combien de triangles semblables sont là?

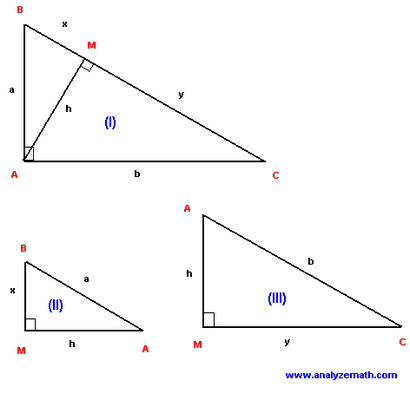
Solution au problème 5:

Considérons les triangles ABC et MBA. Ils ont deux angles congruents correspondants: B. angle et de l'angle droit, ils sont similaires. triangles aussi ABC et MAC ont deux angles congruents: l'angle droit et de l'angle C. Par conséquent, il y a trois triangles semblables: ABC, MBA et MAC.

Triangle Problèmes similaires

Articles Liés