Comment comprendre logarithmes 5 étapes (avec photos)

Connaître la différence entre les équations logarithmiques et exponentielles. Ceci est une première étape très simple. Si elle contient un logarithme (par exemple: Loga x = y) est logarithmique problème. Un logarithme est désigné par les lettres « log ». Si l'équation contient un exposant (à savoir, une variable élevée à une puissance), il est une équation exponentielle. Un exposant est un nombre placé après un superscript nombre.

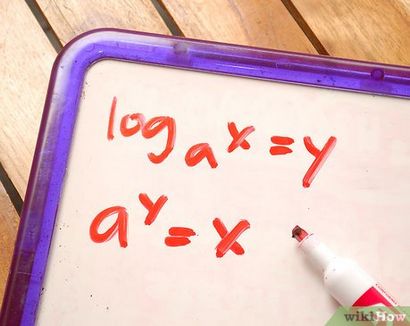
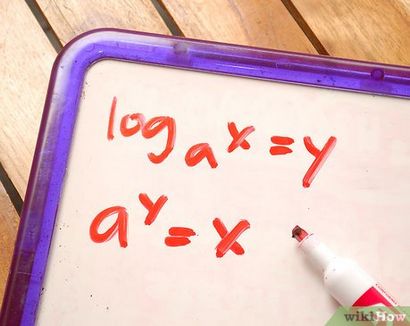
Logarithmique: loga x = y
Exponentielle: y = a x

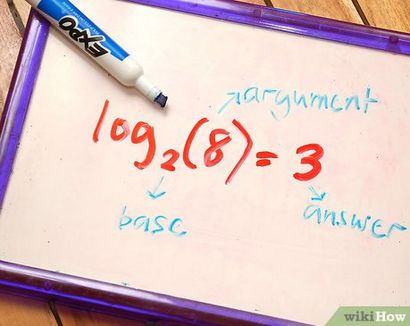
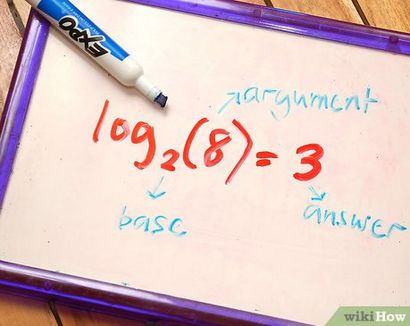
Connaître les parties d'un logarithme. La base est le numéro de trouvé après les indice lettres « log » - 2 dans cet exemple. L'argument ou le numéro est le numéro suivant le numéro de l'indice - 8 dans cet exemple. Enfin, la réponse est le nombre que l'expression logarithmique est égale à - 3 dans cette équation. [2]

Connaître et appliquer les propriétés des logarithmes. Les propriétés de logarithmes vous permettent de résoudre des équations logarithmiques et exponentielles qui seraient autrement impossibles. Ceux-ci ne fonctionnent que si l'un de base et l'argument sont positifs. De plus, le une base ne peut pas être 1 ou 0. Les propriétés des logarithmes sont énumérés ci-dessous un exemple distinct pour chacun des nombres au lieu de variables. Ces propriétés sont à utiliser lors de la résolution des équations.

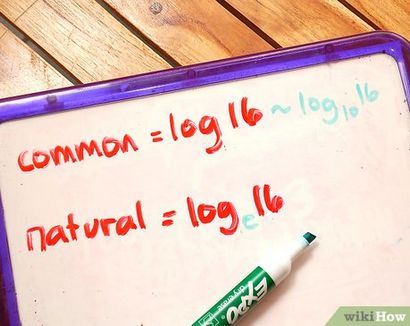
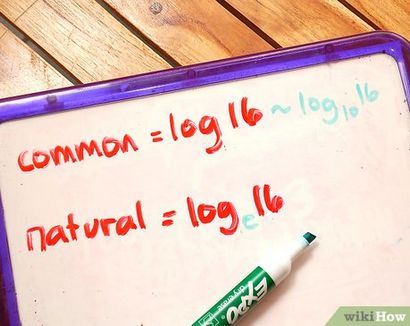
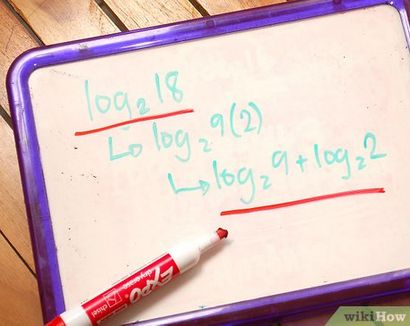
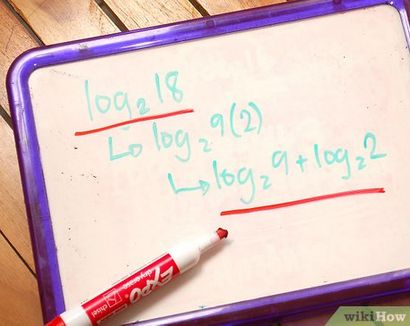
loga (xy) = loga x + y loga
Un journal de deux nombres, x et y. qui sont multipliés par les uns des autres peuvent être divisés en deux journaux distincts: un journal de chacun des facteurs étant additionnés. (Cela fonctionne également en sens inverse.)

Exemple:
log2 16 =
log2 8 * 2 =
log2 8 + log2 2

loga (x / y) = loga x - y loga
Un journal d'un deux nombres étant divisé par l'autre, x et y. peut être divisé en deux journaux: le journal du dividende x moins le journal du diviseur y. Exemple:
log2 (5/3) =
log2 5 - log2 3

loga (x r) = r * x loga
Si l'argument x du journal a un exposant r. l'exposant peut être déplacé vers l'avant du logarithme. Exemple:
log2 (6 5)
5 * 6 log2

loga (1 / x) = x -loga
Pensez à l'argument. (1 / x) est égal à x-1. En gros, cela est une autre version de la propriété précédente. Exemple:
log2 (1/3) = 3 -log2

loga a = 1
Si l'une de base est égal à l'argument de la réponse est 1. Ceci est très facile de se rappeler si l'on pense au logarithme sous forme exponentielle. Combien de fois doit-on multiplier un par lui-même pour obtenir un. Une fois que. Exemple:
log2 2 = 1

loga 1 = 0
Si l'argument est une réponse est toujours égale à zéro. Cette propriété est vrai parce que tout nombre avec un exposant de zéro est égal à un. Exemple:
log3 1 = 0

(Logb x / logb a) = loga x
Ceci est connu comme « Changement de base ». [3] Un journal divisé par une autre, à la fois avec la même base b. est égal à un journal unique. L'un argument du dénominateur devient la nouvelle base, et l'argument x du numérateur devient le nouvel argument. Ceci est facile à retenir si vous pensez à la base que le fond d'un objet et le dénominateur que le fond d'une fraction.

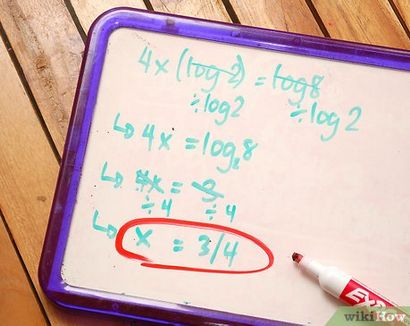
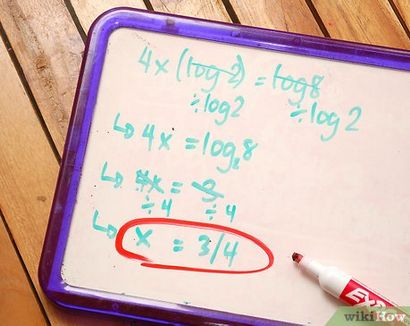
Pratique en utilisant les propriétés. Ces propriétés sont mieux mémorisés par une utilisation répétée lors de la résolution des équations. Voici un exemple d'une équation qui est mieux résolu avec l'une des propriétés:

4x * log2 = log8 Diviser les deux côtés par log2.
4x = (log8 / log2) Changement de base.
4x = log2 8 Calculer la valeur du journal.
4x = 3 Diviser les deux côtés par 4. x = 3/4 Solved. Ceci est très utile. Je comprends maintenant les journaux.

Articles Liés

Précédent ◈ Suivant