Comment représenter graphiquement les équations linéaires 5 étapes (avec photos)

Assurez-vous que l'équation linéaire est sous la forme y = mx + b. On appelle cela la forme ordonnée à l'origine, et il est probablement la forme la plus facile à utiliser pour représenter graphiquement des équations linéaires. Les valeurs de l'équation ne doivent pas nécessairement être des nombres entiers. Souvent, vous verrez une équation qui ressemble à ceci: y = 1 / 4x + 5. où 1/4 est m et 5 b.

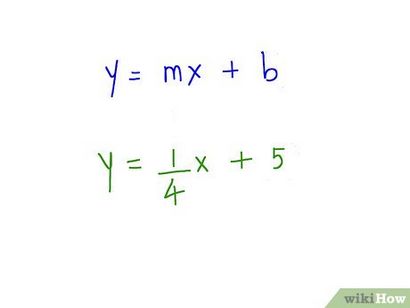
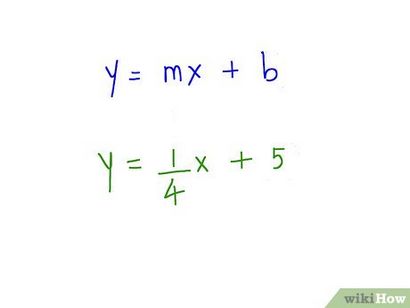
m est appelée la « pente » ou parfois « gradient ». La pente est définie comme étant montée sur la distance, ou la variation de y sur la variation de x.

b est définie comme étant la « ordonnée à l'origine. » L'ordonnée à l'origine est le point où la ligne coupe l'axe des ordonnées.

x et y sont les deux variables. Vous pouvez résoudre pour une valeur spécifique de x. par exemple, si vous avez un point y et connaître les m et les valeurs b. X. cependant, est jamais simplement une valeur: sa valeur change au fur et à haut ou en bas de la ligne.

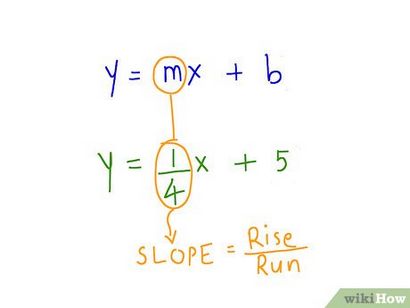
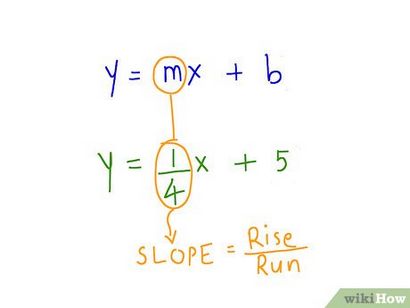
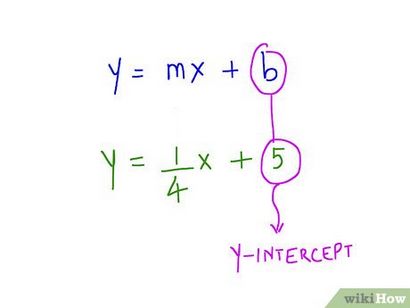
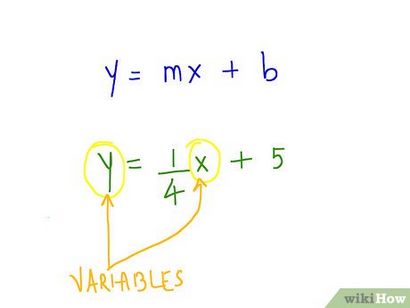
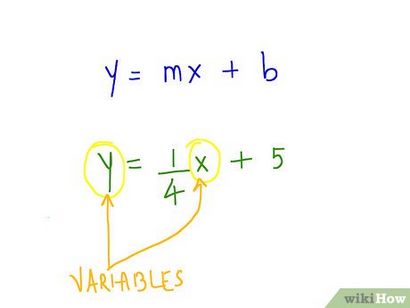
Tracer le nombre de b sur l'axe Y. Votre b va toujours être un nombre rationnel. Juste quel que soit le numéro B est, trouver son équivalent sur l'axe Y, et de mettre le numéro à cet endroit sur l'axe vertical.

Autre m en une fraction. Souvent, le nombre devant x est déjà une fraction, de sorte que vous n'aurez pas à le convertir. Mais si ce n'est pas, le convertir en plaçant simplement la valeur de m sur 1.

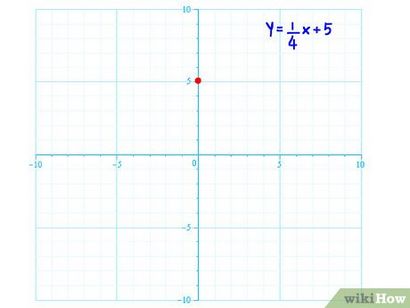
Le premier nombre (numérateur) est la montée en élévation et de course. Il est dans quelle mesure la ligne se déplace jusqu'à, ou verticalement.

Le second nombre (dénominateur) est le centre élévation et de course. Il est dans quelle mesure la ligne se déplace sur le côté, ou à l'horizontale.

Par exemple:

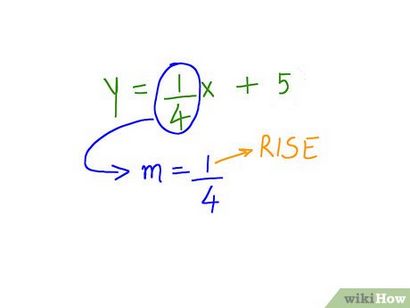
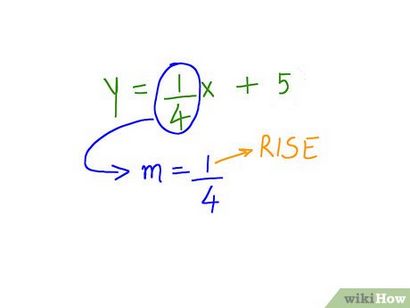
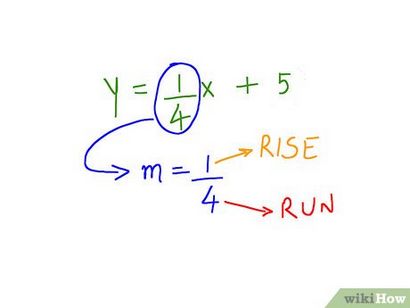
Une pente 01/04 se déplace vers le haut de 4 périodes pour chaque point sur 1.
Une pente -2/1 se déplace vers le bas de 2 points pour chaque point sur 1.
Une pente 1/5 déplace jusqu'à 1 points pour chaque 5 points sur.

Lancer l'extension de la ligne de b en utilisant la pente, ou augmenter au cours de l'exécution. Commencez à votre valeur b: on sait que l'équation passe par ce point. Prolonger la ligne en prenant votre pente et en utilisant ses valeurs pour obtenir des points sur l'équation.

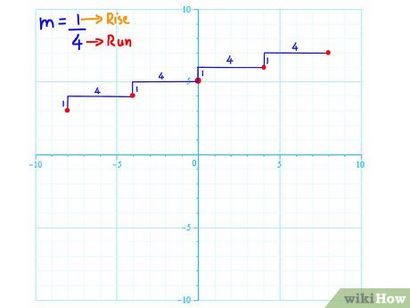
Par exemple, en utilisant l'illustration ci-dessus, vous pouvez voir que pour chaque 1 point, la ligne monte, il se déplace 4 à droite. En effet, la pente de la ligne est de 1/4. Vous prolongez la ligne indéfiniment le long des deux côtés, en continuant à utiliser montée sur la distance pour représenter graphiquement la ligne.
Considérant que les pentes de valeurs positives se déplacent vers le haut, les pentes de valeur négative se déplacent vers le bas. Une pente de -1/4, par exemple, voyagerait en baisse de 1 point pour chaque 4 points, il se déplace vers la droite.

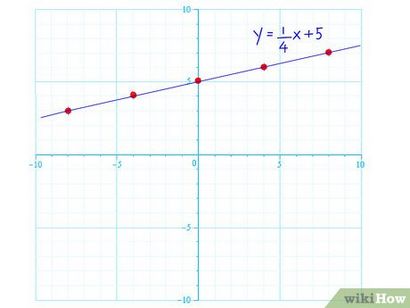
Continuer l'extension de la ligne, en utilisant une règle et d'être sûr d'utiliser la pente m. comme un guide. Prolonger la ligne indéfiniment et vous avez terminé votre équation linéaire graphiquement. Assez facile, non?

Articles Liés

Précédent ◈ Suivant