Division de la fraction par Rectangles
Je vous remercie de poste de Christopher Danielson sur la division fraction de numérateur commun, car il est important d'examiner comment différents algorithmes fonctionnent et comment nous pouvons aider nos étudiants à devenir plus souple avec leur pensée. Il n'est pas surprenant que j'enseigne la division fraction en utilisant des rectangles, et je crois vraiment que les enfants semblent mieux saisir parce qu'il est visuel.
Je vais commencer par ce problème: 3/4 ÷ 2/3.
Mais avant de faire la division fraction, je demande aux enfants sur la division de nombre entier. Qu'est-ce que 8 ÷ 2? Qu'est-ce que 15 ÷ 5? Finalement, nous nous installons sur quelque chose comme: demander ce qui est 8 divisé par 2 est la même chose que demander combien de groupes de 2 à 8 sont.
Ensuite, nous appliquons la même question à 3/4 ÷ 2/3 comme « nombre de groupes de 2/3 sont en 3/4? »
Je les guider à travers ce processus:
Tirons des 3/4 et 2/3 sur le papier.
La moitié d'entre eux dessiner des cercles. Awful, en état d'ébriété, des cercles mal comportés.
Utilisons à la place du papier quadrillé pour dessiner nos rectangles. Je pense que vous pouvez montrer 3/4 beaucoup plus de précision sur du papier quadrillé que sur un cercle.
S'il vous plaît piocher 2 rectangles de même taille. (En faisant cela, nous divisons vraiment deux fractions en utilisant la stratégie de dénominateur commun. Christopher écrit à ce sujet ici.)
Ils demandent, de toute taille?
Quelle taille pensez-vous? Est-ce que ça importe?
Ombre le premier à montrer 3/4 et le second pour montrer 2/3.
Ils gâcher. Ils pourraient dessiner un 1 x 4 rectangle, ombre 3 pour montrer 3/4. Mais ils ne savent pas comment l'ombre dans 2/3 d'un 1 x 4.
Cette invite est assez pour quelqu'un de dire, Dessiner un 4 par 3 rectangle!
Bingo! Je dessine avec vous. Ok, alors deux rectangles de 4 par 3 - ou 3 par 4 - n'a pas d'importance.
Je suis ombrage en 3/4 sur le premier et 2/3 sur le second.
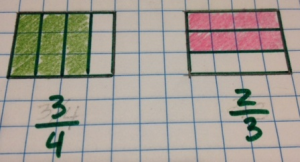
Donc, notre question est: Combien de groupes de 2/3 sont en 3/4?
Parce que je le mien de couleur dans, pouvez-vous me aider à poser à nouveau la question en utilisant des couleurs à la place?
Quelqu'un répond, Combien de roses sont les verts?
Ouais. Et combien de petits carrés sont roses? D'accord, huit.
Alors, je vais vers le vert ici et arrondir 8 carrés roses.
Je suis capable d'arrondir un groupe de 2/3 (rose) dans le 3/4 (vert).
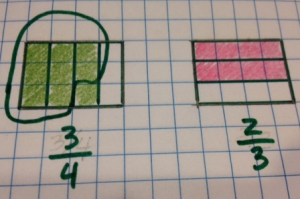
Quelqu'un dit: Il y a un reste.
Combien est-ce une petite place verte à gauche sur la valeur?
Droite! 1/8 parce que nous appelé 8 petites boîtes comme l'un, donc 1 petite boîte doit être 1/8.
Notre réponse est alors 1 et 1/8.
Quelques étudiants disent, je l'obtiens.
Comment savons-nous que notre réponse de 1 1/8 est correcte?
D'accord, nous allons utiliser une calculatrice.
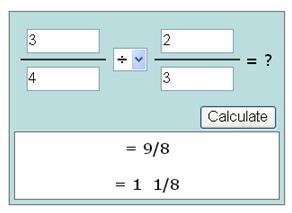
Faisons-le à nouveau. Maintenant, avec un nombre mixte juste pour le plaisir. Faisons 1 1/2 ÷ 2/5.
Combien de rectangles tirons-nous?
Quelles dimensions doivent-ils être?
Oh, mais nous avons plus de 1 tout ici, donc ...?
Nous devrions avoir quelque chose comme ça alors.
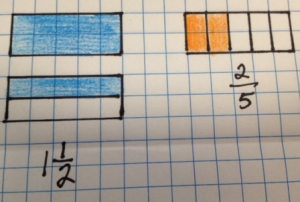
Ils disent: Combien de groupes d'orange sont en bleu?
Permettez-moi de rassembler les groupes d'orange qui sont dans le bleu.
Je suis arrivé trois. Et le restant est? A droite, trois. Trois sur ...?
Plus d'étudiants disent, les trois quarts! Trois et trois quarts. J'ai compris!
Cette calculatrice en ligne permet de Calcul des entrées de nombres fractionnaires.
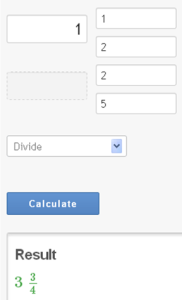
D'accord, votre tour de faire un par vous-même.
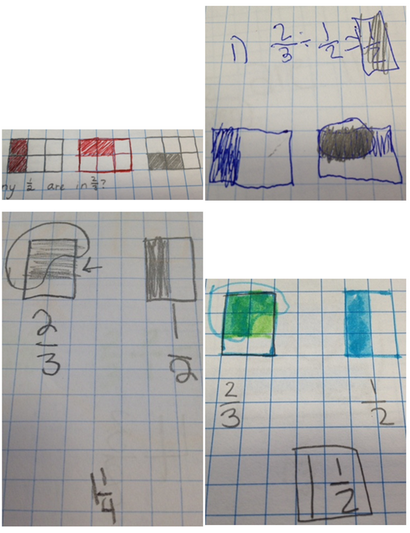
Je pense que les papiers de ces enfants montrent la compréhension.

Bien que ceux-ci ne sont pas encore là.
Je ne sais pas. Mais il semble que dessiner des images et faire des choses plus visuelles commencent à disparaître au collège. Voici notre traitement manuel de « division des fractions et des nombres mixtes » - Chapitre 5, Section 7 - 3 pages pleines avant les exercices. Remarquez les deux cercles au début de la section - qui est à peu près tout. Et les cercles sont très bien si vous avez dénominateurs de 2, 4 et 8.

Je pense que si je peux obtenir mes enfants d'abord voir la réponse, alors je peux les vendre les autres algorithmes - comme multiplier l'inverse - et non apparaître comme une fraude.
Je tiens également à souligner que je vois normalement ce visuel ci-dessous pour la division des fractions. Mon chemin est différent - je demande délibérément les enfants à dessiner 2 rectangles dont les dimensions sont les dénominateurs.
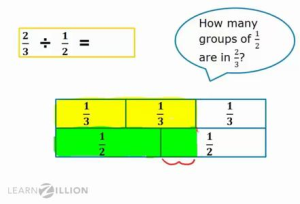
Merci à Rachel Emily Tabak pour la création de cette feuille d'accompagnement, 18 - rectangles de division Frac.
Fawn - Merci beaucoup pour le partage. J'apprécie vraiment vos idées et comment bien vous les poser pour le reste d'entre nous. J'ai passé un peu de temps avec les étudiants division représentant visuellement plus tôt dans l'année (bien que je trouve votre façon plus intuitive). Les étudiants semblaient avoir. Je puis « les vendais un algorithme » - Comment ramifier-vous de l'algorithme réciproque se multiplient? - et tout semblait très bien. Récemment, je travaillais division en arrière et un étudiant fort m'a regardé comme si elle n'a jamais été discuté. Je me sens bien ... ouais, mais je me demandais si vous revenir à des rectangles ou faire ce à ce moment.
Après les rectangles, je leur montre la division dénominateur commun, car ils sont déjà trouver des dénominateurs communs pour additionner et soustraire. Je voudrais aussi ne se multiplient l'inverse. Ce sont facile à vendre après avoir vu les rectangles, je pense. Merci beaucoup, Frank, pour vos aimables paroles.