Équations linéaires INTERCEPTE, Standard et Graphing - Vidéo & Transcript Leçon
Savez-vous quoi faire si une équation ne ressemble pas à y = mx + b. Sinon, cette vidéo est pour vous. Les chances sont l'équation est sous forme standard, donc nous allons apprendre comment utiliser des équations de forme standard comment les représenter graphiquement et pourquoi ils peuvent être utiles.
Comment convertir le format standard
Cette vidéo est sur les différentes formes d'une équation linéaire. en particulier sous forme d'une pente et la forme standard, et comment nous pouvons tracer des lignes qui nous sont donnés dans l'une de ces formes. sous forme d'une pente (y = mx + b) est celui que la plupart des gens sont familiers avec. Il est le plus commun que vous voyez, mais cela ne veut pas dire qu'il est la seule façon de représenter une équation linéaire.
Par exemple, si j'avais la ligne y = 3x +4, qui m'a été donnée sous forme d'une pente, en utilisant les opérations inverses et en prenant un 3x positif et défaisant avec une -3x des deux côtés, je me retrouve avec l'équation - 3x + y = 4. Ces deux équations sont équivalentes. Ils veulent dire la même chose. Ils sont la même chose, ils sont juste écrits différemment. Ce que je finis avec dans ce second est ce qu'on appelle la forme standard. Essentiellement, parce que les x et y s s sont sur le même côté de l'équation. L'équation de la forme de type générique est Ax + By = C.
La conversion d'une équation à partir de la pente à l'origine de forme standard

Ceci est probablement la deuxième forme la plus courante d'une équation linéaire que vous voyez, mais à la différence sous la forme pente-ordonnée à l'origine, l'As et ne nous donnent hôtes pas nécessairement toutes les informations utiles comme les m et b fait sous la forme d'une pente. Cela ne signifie pas qu'il n'y a pas encore des avantages à la forme standard sur la forme d'une pente.
Way « pente Intercept » pour représenter graphiquement une équation linéaire
Ce que nous allons savoir est que l'orientation des variables sous forme standard permet de trouver x et y -intercepts assez rapide et facile, ce qui nous permettra d'utiliser une sorte de raccourci quand il s'agit de graphique.
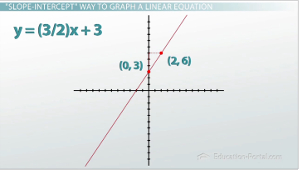
Ici, nous avons une question qui nous demande de représenter graphiquement la ligne -3x + 2y = 6. Alors, faisons la façon dont nous savons à quel point, ce qui est à l'aide sous forme d'une pente à utiliser la valeur m et la valeur b pour représenter graphiquement notre ligne. Mais parce que cela ne nous est pas donnée sous forme d'une pente, il nous faut d'abord le mettre sous forme d'une pente en utilisant les opérations inverses pour obtenir l'y par lui-même. Cela signifie que nous devons d'abord défaire le -3x avec un 3x positif pour les deux parties; nous devons annuler une fois par 2 avec une division par 2 des deux côtés. Maintenant, nous avons l'équation y = (3/2) x 3. Cette équation est équivalente à celle que nous avons commencé avec, vient d'écrire d'une manière différente.
Trouver la forme d'une pente
Maintenant qu'il est écrit sous forme d'une pente, je sais que je peux utiliser mon m (ma pente) et mon b (mon ordonnée à l'origine) pour la représenter graphiquement. Je commence à 3 sur la y -axis, puis je monte 3 et plus de 2 pour trouver mon point suivant en utilisant la pente. Vous pouvez continuer à monter 3 et plus de 2 autant de fois que vous voulez, mais vous remarquerez que tous vos points sont dans la même ligne droite. Vous pouvez connecter cette ligne et vous avez votre graphique. Ce qui est pas trop mal, mais ces étapes du début qui nous doit d'abord obtenir l'y par lui-même sont, en particulier avec les fractions inutiles et parfois ils peuvent être un peu compliqué. Nous préférerions savons un moyen de le faire sans avoir à résoudre pour y.
Graphique de l'équation linéaire y = (3/2) x + 3
Way « Standard » pour représenter graphiquement une équation linéaire
Donc, nous allons jeter un oeil à exactement le même problème: graphique -3x + 2y = 6. Mais cette fois, essayez de le faire sans avoir à faire par lui-même toutes les étapes commençant où nous obtenons y en utilisant des opérations inverses et avoir à traiter avec des fractions et tout ce genre de choses en désordre.
Nous savons que le x ordonnée à l'origine, y est 0, et à l'ordonnée à l'origine, x est égal à 0. Donc, parce que nous savons, il se trouve que x et y -intercepts sont vraiment faciles à trouver. Vérifiez-le; si je sais que le x à y est ordonnée à l'origine 0, je peux simplement remplacer 0 en pour y dans mon équation, ce qui me donne -3x + (2 * 0) = 6.
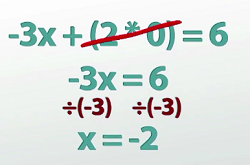
Collège de crédit Gagner
Saviez-vous que ... Nous avons plus de 95 cours de niveau collégial que vous vous préparez à gagner le crédit par l'examen qui est acceptée par plus de 2000 collèges et universités. Vous pouvez tester des deux premières années de collège et de sauver des milliers de votre diplôme. Tout le monde peut gagner des crédits par examen quel que soit l'âge ou le niveau d'éducation.
Transfert de crédit à l'école de votre choix
Je ne sais pas ce que l'université vous voulez assister encore? Study.com a des milliers d'articles sur tous les degrés imaginables, domaine d'études et de carrière qui peut vous aider à trouver l'école qui est bon pour vous.
Écoles de recherche, grades - Carrières
Obtenez les informations impartiales vous devez trouver la bonne école.