Formulaire pente Intercept - Lignes Représentation graphique - Math gratuit Aide
Il est une méthode standard pour écrire l'équation d'une ligne. Il a deux variables, x et y, et un nombre illimité de « solutions » (la ligne est infiniment longue).
À quoi cela ressemble-t-il?
Une ligne écrite sous forme d'une pente prend cette forme:
Parfois, vous pourrez même entendre les gens se réfèrent à la pente à l'origine comme « y = mx + b » parce qu'il est si bien connu. Examinons ce que signifie chaque terme. Rappelez-vous que vous complotez ce graphique sur un plan x-y, de sorte que les variables x et y représentent des points géométriques sur le graphique. Le « m » constante est la pente du graphique - remarquez comment il multiplie votre x terme. En effet, la pente d'un graphique détermine combien « y » change en fonction de « x ». Le dernier terme, b, est l'ordonnée à l'origine. C'est le point où la ligne coupe l'axe des y, où x = 0. Si vous branchez 0 pour x, vous verrez que tout ce que vous avez est y = b.
Un exemple:
Q: Tracer la ligne décrite par l'équation suivante: \ (y = x + 1 \)
R: Quelle est la pente de cette ligne? Il est le terme 'm' y = mx + b. Dans cet exemple, m = 1. Par conséquent, la pente de la ligne est 1, ou dit d'une autre manière, la ligne va « jusqu'à » une unité à chaque fois qu'il va « sur » une unité.
Quelle est l'ordonnée à l'origine de la ligne? C'est le « b » terme, il est donc aussi 1. Cela signifie que lorsque x est 0, y = 1. Allez-y et branchez x = 0 dans cette équation pour vérifier par vous-même.
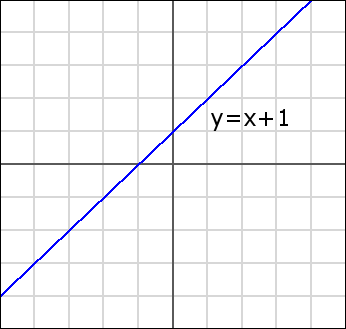
Dans cet exemple, notez comment la ligne croise l'axe des y (axe vertical) en y = 1? C'est la partie « interception » de la forme d'une pente.
Voyons voir quelque chose de plus compliqué.
L'exemple suivant aura des chiffres plus compliqués. Cependant, il est toujours aussi simple que de les lire à partir de l'équation et de travail par étape par étape.
Q: Tracer la ligne \ (y = 2x - 5 \)
R: Ok, donc ce qui est la pente? Que le « m », et multiplie les x. Dans ce cas, il est 2. Quelle est l'ordonnée à l'? Notez qu'il est soustraite, de sorte que l'ordonnée à l'est en fait -5.
Ok, alors comment voulez-vous tracer réellement que ??
Vous pouvez commencer à partir de la ordonnée à l'origine. Nous savons que la ligne traverse l'axe y à \ (y = -5 \), de sorte que vous pouvez tracer le point \ ((0, -5) \).
Ensuite, étant donné que la pente est 2, vous devez monter deux unités pour chaque 1 vous allez sur:
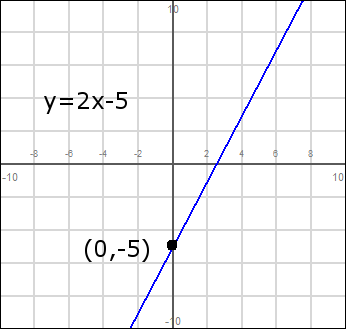
Ok, donc vous comprenez les bases maintenant? Il suffit de trouver l'ordonnée à l'origine, puis tracer une ligne avec la pente donnée.
Mais, parfois l'équation ne sera pas dans un format facile à lire \ (y = mx + b \) format. Parfois, il se penchera plus compliqué. Tout ce que vous avez à faire est de réécrire l'équation en cette forme, comme ceci:
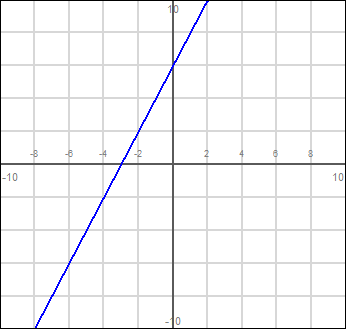
Ré-écriture en forme de point pente:
A: Récrivez au format \ (y = mx + b \). Multiplier le 2 sur la parenthèse:
Maintenant, nous sommes dans le bon format, et nous pouvons facilement le tracer
Parfois, vous verrez x et y sur le même côté de l'équation, ou un terme qui y multiplie, comme cet exemple méchant:
Comme avant, il suffit d'utiliser vos connaissances de l'algèbre de base pour réécrire en \ (y = mx + b \) Format:
$$ 4y + x = 12 $$ $$ 4y = -x + 12 $$ $$ y = -.25x + 3 $$