Jeux non transitif, Dan Q
dés non transitif
Avez-vous déjà rencontré des dés non transitif. Le jeu classique, que vous pouvez obtenir dans la plupart des magasins de magie, se compose de trois dés à six faces de différentes couleurs:

Un style « de Grime » un ensemble de 3 dés non transitif. Remarquez la numérotation inhabituelle.
Il existe plusieurs variantes, mais une commune, comme indiqué par James Grime. implique une matrice de cinq « 3 » côtés et une « 6 » côté (décrit comme rouge ci-dessous), une seconde matrice avec trois côtés « 2 » et trois côtés « 5 » (décrit comme vert ci-dessous), et une troisième matrice avec une côté « 1 » et cinq côtés « quatre » (comme décrit ci-dessous bleu).
Ils sont tous les dés justes, et - comme un dé à six faces normales - ils ont tous un score moyen de 3,5. Mais ils ont une propriété intéressante, que vous pouvez utiliser pour toutes sortes de tours de magie et des jeux de hasard. En règle générale: la filière rouge va battre la filière verte, la filière verte va battre le dé bleu, et la matrice bleue battre le dé rouge! (Pensez Rock, papier, ciseaux ...)
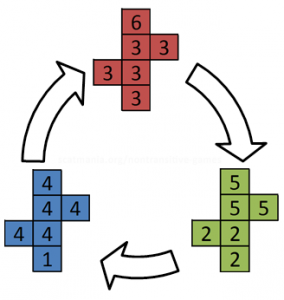
Apparemment, paradoxalement, les dés vont battre en général un autre dans un motif circulaire.
Mais si cela ne vous suffit pas cuire au four de nouilles, essayez de récupérer deux jeux de dés et non transitives essayer à nouveau. Maintenant, vous verrez que le motif inverse: la paire verte a tendance à battre la paire rouge, la paire rouge a tendance à battre la paire bleue, et la paire bleue a tendance à battre la paire verte! (Ce qui en fait un grand deuxième acte à vos efforts pour toison quelqu'un de leur argent dans un jeu de jeu: une fois qu'ils ont travaillé sur la façon dont vous continuez à gagner, leur donner la chance d'aller « double ou rien », en utilisant deux dés, et vous offre même de choisir d'abord!)
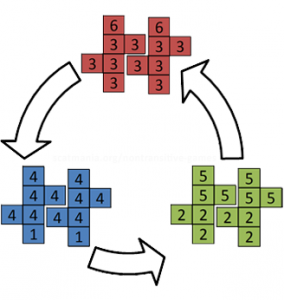
Lorsque vous associez les dés, le cycle inverse! Alors que beats rouge, vert beats double vert double rouge!
Les propriétés de ces dés - et des formes les plus exotiques, comme l'ensemble de sept dés d'Oskar van Deventer (approprié pour jouer un jeu avec trois joueurs et battre vos deux adversaires) et comme les variétés polyèdres discutées sur Wikipedia - intriguer le jeu théoricienne et jeux de société concepteur en moi. Y aurait-il le potentiel de ce mécanicien d'exister dans un jeu de société? Je pense quelque chose avec le risque, comme le combat (dés « knock out » un autre du plus élevé au plus bas), mais avec un mécanicien « d'acquisition dés » (afin que les joueurs effectuent des actions, peut-être dans un format d'enchères, d'acquérir dés de couleurs particulières - chacun avec leurs propres forces et faiblesses des autres dés - pour soutenir leur « main » de dés). Il y a une discussion en cours dans / r / tabletopgamedesign ...
J'ai même écrit un programme (que vous êtes invités à télécharger, adapter et utilisation) pour calulate les chances de toute combinaison de variété de dés non transitif uns contre les autres, ou même pour vous aider à développer votre propre non transitif jeux de dés.
jeu de Penney
Pile ou face? Avec l'aimable autorisation David M. Diaz.
Voici un autre jeu non-transitif pour vous, mais cette fois: Je l'ai fait dans un réel jeu jouable que vous pouvez essayer en ce moment. Dans ce jeu, vous et moi chacun, à son tour, prévoir trois flips consécutifs d'une pièce de monnaie - de sorte que vous pourriez prévoir « queues, têtes, têtes ». Ensuite, nous allons commencer lancer une pièce, encore et encore, jusqu'à ce que l'une de nos séquences arrive. Et plus souvent qu'autrement, je vais gagner.
Si vous gagnez 10 fois (ou vous perdez 20 fois, ce qui est plus probable!), Je vais vous expliquer comment le jeu fonctionne, vous savez comment je « triché ». Je vais vous rappeler: les flips de pièces sont justes, et il n'y a rien à voir avec un ordinateur - si nous avons joué ce jeu face à face, avec une vraie pièce, je serais encore gagner. Maintenant, allez jouer!