loi de vitesse intégrale, la demi-vie
Sur cette page, nous étendons le concept de lois de taux différentiels présentés à la page précédente aux lois de taux et intégrantes réaction demi-vie qui sont d'une grande importance dans les applications les plus pratiques de la cinétique.
Différentiel et lois de vitesse intégrale
La loi de taux de droit commun (plus précisément connu comme la loi de vitesse instantanée ou différentiel) nous indique la vitesse d'une réaction dépend de la concentration des réactifs. Mais pour de nombreuses raisons pratiques, il est plus important de savoir comment les concentrations de réactifs (et des produits) changent avec le temps.
Par exemple, si vous effectuez une réaction à l'échelle industrielle, vous voulez savoir combien de temps il faudra pour, disons, 95% des réactifs à convertir en produits.
Tel est l'objet d'une loi tarifaire intégrée.
L'intégration de la loi sur les taux
Cela est facile à faire, mais seulement quelques cours vous attendent de savoir comment le faire. Pour une course rapide sur site, cliquez ici. Si vous avez eu même un peu de calcul, voici l'occasion de les mettre à profit!
Exprimant la « vitesse » d'une réaction: la demi-vie
Combien de temps faut-il pour une réaction chimique de se produire dans un ensemble de conditions? Comme de nombreuses questions « simples », aucune réponse significative ne peut être donnée sans être plus précis. Dans ce cas,
Comment peut-on définir le point où la réaction est « terminée »?
Si la constante d'équilibre est assez grand, alors la réponse réduit à une forme plus simple: la réaction est terminée lorsque la concentration d'un réactif tombe à zéro. Dans un souci de simplicité, nous supposons que cela est le cas dans le reste de cette discussion.
La fraction particulière on choisit dépend du coût des réactifs par rapport à la valeur des produits, équilibrés par rapport au coût de fonctionnement du processus pour un temps plus ou l'inconvénient d'attendre plus de produits. Ce genre de considération est particulièrement imporant dans les procédés industriels dans lesquels les soldes de ces coûts affectent la rentabilité de l'opération.
La demi-vie d'une réaction
Au lieu d'essayer d'identifier le temps nécessaire à la réaction de devenir terminé, il est beaucoup plus pratique de préciser le temps nécessaire à la concentration d'un réactif à tomber à la moitié de sa valeur initiale. Ceci est connu comme la demi-vie (ou mi-temps) de la réaction.
réactions de premier ordre
La loi du changement exponentielle
La vitesse à laquelle un réactif est consommé dans un processus du premier ordre est proportionnelle à sa concentration à ce moment. Cette relation générale, dans laquelle une quantité change à une vitesse qui dépend de sa valeur instantanée. est dit de suivre une loi exponentielle.
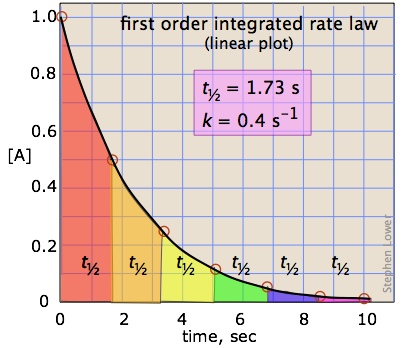
Le premier ordre loi de vitesse intégré
A produits →
est un exemple courant de la loi du changement exponentielle. Pour un corps réactionnel A, la concentration [A] t à l'instant t est donnée par
dans laquelle [A] o est la concentration initiale et k est le premier ordre constante de vitesse.
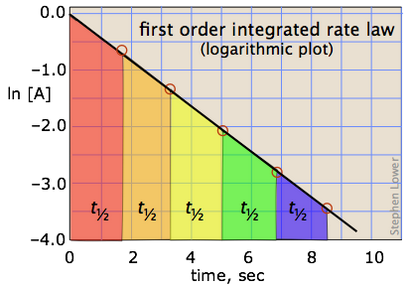
Cela a la forme d'une équation pour une ligne droite
Après une période d'une demi-vie, t = t½ et nous pouvons écrire
(Dans lequel nous exprimons l'exponentielle en fonction afin de faire ressortir une place plus importante.) En prenant logarithmes des deux côtés (rappelez-vous que
ln e x = x) les rendements
La résolution de la demi-vie, on obtient la relation simple
qui nous dit que la demi-vie d'une réaction de premier ordre est une constante. Cela signifie que 100.000 molécules d'un réactif sera réduit à 50 000 dans le même intervalle de temps nécessaire pour dix molcules être réduit à cinq.
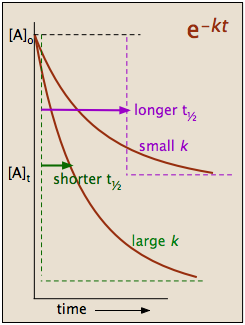
Il devrait être clair que la constante de vitesse et la demi-vie d'un processus de premier ordre sont inversement proportionnels.
La demi-vie d'une réaction du premier ordre a été trouvée comme étant de 10 min à une certaine température. Quelle est sa constante de vitesse en quelques secondes réciproques?
L'isotope de masse 241 de l'américium, largement utilisé comme source d'ionisation dans les détecteurs de fumée, a une demi-vie de 432 ans.
c) Quelle serait la « septième vie » de 241 Am?
réactions de second ordre
L'intégration de la loi de vitesse de second ordre
La demi-vie est donnée par
(Voir ici pour plus de détails)
Notez que la demi-vie d'une réaction de second ordre dépend de la concentration initiale, par opposition à sa constance pour une réaction de premier ordre. Pour cette raison, le concept de demi-vie pour une réaction de second ordre est beaucoup moins utile.
processus d'ordre zéro
Dans certaines réactions, le taux est apparemment indépendant du concentraton réactif, auquel cas
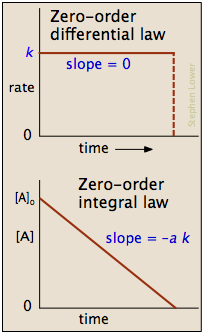
Remarque dans la phrase précédente le mot « apparemment »; cinétique d'ordre zéro est toujours un artefact des conditions dans lesquelles la réaction est mise en oeuvre. Pour cette raison, les réactions qui suivent une cinétique d'ordre zéro sont souvent désignés comme des réactions d'ordre pseudo-zéro.
De toute évidence, un processus d'ordre zéro ne peut pas continuer après un réactif a été épuisé. Juste avant ce point est atteint, la réaction revenir à une autre loi de vitesse au lieu de tomber directement à zéro comme cela est représenté en haut à gauche.
Il y a deux conditions générales qui peuvent donner lieu à des taux d'ordre zéro:
- Seule une petite fraction des molécules de réactif sont dans un endroit ou un état dans lequel ils sont capables de réagir, et cette fraction est réapprovisionné en permanence de la plus grande piscine.
Cette situation se produit généralement quand une réaction est catalysée par la fixation à une surface solide (catalyse hétérogène) ou à une enzyme.
en présence d'un fil de platine chaude (qui agit comme un catalyseur) est d'ordre zéro, mais il suit une cinétique plus conventionnels lorsqu'il est effectué entièrement dans la phase gazeuse.
Ceci est le plus souvent observé lorsque deux ou plusieurs réactifs sont impliqués. Ainsi, si la réaction
est du premier ordre dans les deux réactifs de telle sorte que
vitesse = k [UN B]
alors si B est présent en grand excès, la réaction semble être d'ordre zéro en B (et premier ordre général). Cela se produit généralement lorsque B est H2 O et la réaction est effectuée en solution aqueuse.
Le tableau suivant compare les paramètres de vitesse de zéro-, de première, et des réactions de deuxième ordre de la forme A → A produits. Voir aussi cette excellente page à partir de l'Université Purdue qui montre des parcelles de [A], ln [A] et 1 / [A] pour chaque commande de réaction.