Mathématiques Illumination, Unité 7, 7
DISTRIBUTION
Rappelons que dans nos exemples précédents les bacs au milieu avaient des probabilités plus élevées que ne les bacs sur les côtés. En effet, il y a plus de chemins qui se terminent dans les bacs moyens que se terminer dans les bacs latéraux. Faisons un histogramme qui est en corrélation avec les bacs et leurs probabilités.
Tout d'abord une machine simple 2 rangs:
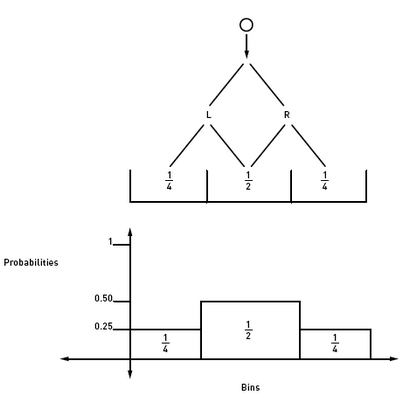
Notez que la distribution est symétrique; les probabilités pour les deux l'extrême droite et l'extrême gauche des bacs sont égaux. Regardons l'histogramme pour une carte Galton avec quatre lignes.
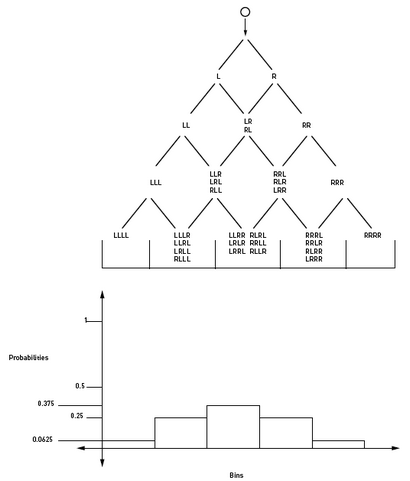
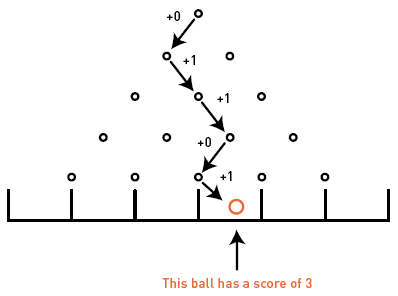
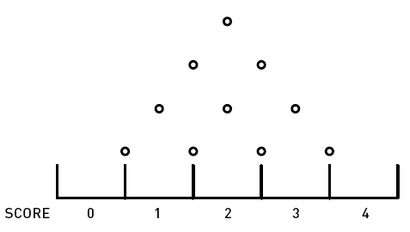
x - m dans laquelle x = valeur attendue et m = moyenne
Parce que cette quantité est quelque chose comme une notion de distance, nous le carré pour faire en sorte que la valeur ne sera pas négatif.
On multiplie ensuite cette différence au carré par la probabilité de se retrouver dans ce bac.
Enfin, si l'on additionne tous ces termes, nous allons obtenir un numéro qui décrit comment sont répartis les valeurs attendues des bacs autour de la moyenne. Ceci est connu comme la variance.
Parce que la variance est basée sur le carré de la différence entre le résultat et la valeur attendue, il adapte un peu maladroitement.
Le nombre de cases correspond au nombre de lignes dans le système. Appelons ce nombre n. Notez que le score maximum est également n. Rappelez-vous que cette configuration peut représenter de nombreuses situations différentes, comme le résultat des lancers de pièces n, ou toute autre situation, peu importe si oui ou non les chances de chaque épreuve individuelle sont 1 à 1, parfois appelé comme « 50-50 hasard « .
INCLINAISON DU CONSEIL
- Si nous attribuons une probabilité autre que de chaque pion du conseil Galton, la moyenne de la distribution se déplacera.
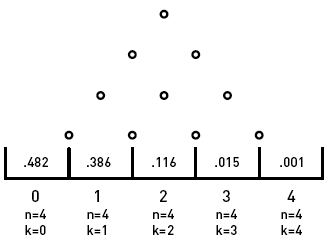
Dans notre système à quatre rangées, nous savons qu'il ya quatre chemins possibles à bac 1. Maintenant, au lieu de regarder le rapport entre le nombre de chemins qui se terminent dans le bac 1 au nombre total de pistes pour trouver la probabilité de se retrouver dans bin 1, on peut penser à la probabilité de chaque trajet spécifique se produise. Chaque voie est une séquence de quatre événements, et chaque événement est soit à gauche (L) ou changement de direction à droite (R). Les quatre voies à bac 1 sont donc, LLLR, LLRL, LRLL, RLLL. La probabilité pour chacun de ces chemins est le produit des probabilités des événements individuels de la séquence. Par exemple: le chemin LLLR a une probabilité de () () () (). Le chemin RLLL a la probabilité () () () (). Notez que tous les chemins à bac 1 ont la même probabilité. Par conséquent, pour trouver la probabilité de se retrouver dans le bac 1, nous pouvons simplement ajouter les probabilités de prendre les chemins d'accès spécifiques qui se terminent dans le bac 1. Étant donné que toutes ces probabilités sont les mêmes, nous pouvons simplement multiplier la probabilité pour un chemin,, fois le nombre de chemins (4) pour obtenir.
On peut généraliser cette réflexion pour arriver à une expression qui nous dira la probabilité d'atterrissage dans le k-ième bac d'un système à n lignes, où la probabilité d'aller à droite à chaque cheville est p et la probabilité d'aller la gauche est le 1-p. On multiplie le nombre de chemins,. fois la probabilité d'aller à droite, p. à la k-ième puissance, fois la probabilité d'aller à gauche, (1-p) à la (n-k) ième puissance (parce que si vous allez à droite k fois, vous allez nécessairement quitté le reste du temps). La probabilité d'atterrissage dans le k ème bac est alors:
× p × k (p-1) (n-k)
Ainsi, la probabilité de décalage à chaque pion à partir de à la fois se déplace toute la distribution des probabilités vers la gauche et décale la valeur moyenne de 2 à. Nous voyons maintenant comment la probabilité de chaque événement (tour) détermine la répartition globale des résultats des événements répétés (séquences de tours).
Non seulement le quart de travail moyenne, mais la variance et le décalage de l'écart-type ainsi. Rappelons que ces valeurs ont à voir avec la façon dont les résultats sont distribués autour de la moyenne. Cette répartition des probabilités ou des résultats, est appelée la distribution binomiale, et il est une distribution courante sous séquences d'événements répétés où il n'y a que deux résultats possibles pour chaque événement.
68-95-97.5
- La distribution normale est une distribution idéale qui est déterminée seulement par sa moyenne et écart-type.
La distribution binomiale est utile, mais il peut prendre un certain temps pour calculer, en particulier dans les situations où n. le nombre d'événements, ou le nombre de lignes dans le système, est grande. Il y a une approximation de cette distribution, cependant, qui est beaucoup plus facile à calculer et qui fournit un modèle assez bon pour la distribution de probabilité. Il peut être trouvé en utilisant uniquement la moyenne et l'écart-type, et il est connu comme la distribution normale, familière à beaucoup d'entre nous comme la « courbe en cloche ».
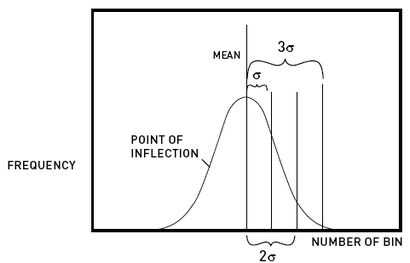
L'approximation de distribution normale fournit un outil puissant pour prédire comment les résultats des expériences indépendantes répétées seront distribués. En outre, plus les événements dans l'ordre que nous regardons, plus la distribution normale est de décrire nos résultats. Bien sûr, il peut toujours des valeurs aberrantes, comme une chaîne de toutes les têtes ou queues, qui momentanément fausseront la distribution d'une façon ou l'autre. Cependant, en moyenne, la distribution normale est assez représentatif du monde réel. En termes de notre conseil d'administration Galton 50-50, qui peut modéliser une variété de situations binaires, cela signifie que plus les lignes que nous avons, plus notre réseau de distribution sera de la distribution normale. La raison sous-jacente implique le théorème central limite, et il est à ce concept que nous allons maintenant.