quinconces Explained

Un Quinconce ou le « conseil Galton » (du nom de Sir Francis Galton) est un réseau triangulaire de chevilles (un jeu avec elle).
Les balles sont déposés sur la cheville du haut, puis rebondir leur chemin vers le bas où ils sont rassemblés dans des petits bacs.
Chaque fois qu'une balle touche l'un des piquets, il rebondit à gauche ou à droite.
Mais ce qui est intéressant: quand il y a une chance égale de rebondir à gauche ou à droite, puis les balles collectées dans les bacs forment la courbe classique « en forme de cloche » de la distribution normale.
(Lorsque les probabilités ne sont même pas, nous obtenons une belle version « biaisée » de la distribution normale.)
Nous pouvons calculer réellement les probabilités!
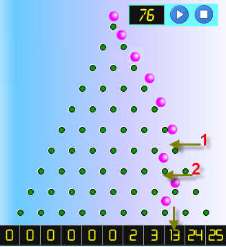
Réfléchissez à ceci: une balle finit dans le bac k places de droite quand il a pris kleft tours.
Dans cet exemple, tous les rebonds sont à droite, sauf pour deux rebonds à gauche. Il a fini dans les deux lieux bin de la droite.
Dans le cas général, lorsque le quinconces a n lignes alors la balle peut avoir bounces k à gauche et (n-k) rebondit à droite.
La probabilité est habituellement de 50% soit, mais il pourrait être de 60% à 40%, etc.
Ainsi, lorsque la probabilité de rebondir à gauche est la probabilité p à droite est (1-p) et nous pouvons calculer la probabilité d'une voie comme ceci:
Le ballon rebondit k fois vers la gauche avec une probabilité de p. p k