Spirale de Theodorus, joueur Russell
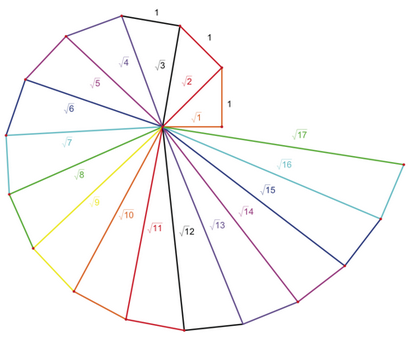
La spirale de Theodorus
Voici quelque chose que je découvre tout en faisant une mission géométrie avancée.
Je devais construire la longueur √3 et je ne pouvais pas pour la vie de me penser à la façon de le faire ... (je me suis souvenu plus tard, mon ami et sa règle Pythagore et ainsi a pu construire un triangle rectangle avec des côtés 1 - √ 3 et une hypoténuse de 2 ... mais au moment où j'étais dans une panique bien!)
Quoi qu'il en soit, dans mes voyages frénétiques je suis tombé sur cette belle construction appelée la spirale de Theodorus.
Maintenant Theodorus était un élève de Protagoras et le tuteur de Platon, l'enseignement des mathématiques. Il a également été membre de la société de Pythagore.
Theodorus était l'un des principaux philosophes de l'école Cyrénaïque de la philosophie morale. Il croyait que les plaisirs et les peines ne sont ni bonnes ni mauvaises. Gaieté et de la sagesse, il croyait, étaient suffisantes pour le bonheur.
Non gars qui croit que peut être tout mal maintenant peut-il?
Il va un peu comme ça ...
- vous construire un 1, 1, √2 triangle, Appelons ce triangle A
- Construire une ligne perpendiculaire, de longueur 1, à partir du point le plus haut sur le triangle A.-à-dire l'un des points où l'hypoténuse rencontre une branche du triangle.
- Joignez-vous à la fin de cette ligne nouvellement construite à l'autre point sur le triangle A. Ce a construit votre deuxième triangle, permet d'appeler son B, et si vous prenez quelques secondes pour faire le calcul, vous serez heureux de découvrir que la longueur de l'hypoténuse du triangle B est ... √3 ... génial hein!
Répétez les étapes 2 - 3 sur chaque triangle consécutif et vous constaterez que le modèle continue à garder sur. Donc, si pour une raison quelconque vous avez besoin de tracer une ligne qui était la longueur ... disons √146 ... vous pouvez simplement dessiner un triangle rectangle avec des côtés 1 - 12, ce qui aura un hypoténuse √145, puis effectuez cette construction une fois de plus et le tour est joué ... une hypoténuse de √146.
Montrer que les enfants et les inciter à dire les mathématiques n'a aucune utilité pratique.