Valeur Singulier décomposition Partie 1 Perspectives sur l'algèbre linéaire, mathématiques ∩ Programmation

Je veux passer le premier poste entièrement sur la motivation et le fond. Dans le cadre de cela, je pense que nous avons besoin d'un petit rappel sur la façon dont l'algèbre linéaire et linéaire tergiverse sous-espaces matrices. Je dis « je pense » parce que ce que je vais dire semble rarement orthographié en détail. En effet, je me suis confus quand j'ai commencé à lire sur l'algèbre linéaire appliquée à des algorithmes, l'apprentissage automatique, la science et de données, en dépit d'une solide compréhension de l'algèbre linéaire d'un point de vue mathématique. Le problème est le lien entre les matrices des transformations et des matrices comme un moyen « pratique » pour organiser les données.

Données par rapport à des cartes

Les amateurs d'algèbre linéaire comme pour exprimer des faits profonds par des déclarations sur factorisation de la matrice. Autrement dit, ils vont dire quelque chose d'opaque comme (ce qui est la déclaration complète pour SVD nous y reviendrons dans le poste):

La SVD d'une matrice avec des valeurs réelles est une factorisation que, le cas est une matrice orthogonale, est une matrice orthogonale, et est une matrice diagonale avec des entrées réelles non négatives sur la diagonale.

D'accord, je peux comprendre les mots individuellement, mais qu'est-ce que cela signifie en termes de la grande image? Il y a deux interprétations apparemment contradictoires des matrices qui brouillent notre vision.

La première est que est une carte linéaire de l'espace vectoriel à n dimensions à un quelconque de dimension. Travaillons avec des nombres réels et appellent l'espace vectoriel de domaine et le codomaine. Dans cette interprétation, la factorisation exprime un changement de base dans le domaine et codomaine. Plus précisément, exprime un changement de base de la base habituelle à une autre base, et fait la même chose pour le co-domaine.

La manière dont ces deux idées se combinent est que les données est considérée comme l'image des vecteurs de base sous la carte linéaire spécifiée par. Voici un exemple pour faire ce béton. Disons que je veux exprimer les films de notation. Chaque ligne correspond aux évaluations d'un film, et chaque colonne correspond à une personne, et l'entrée de la matrice est la personne de notation donne au film.

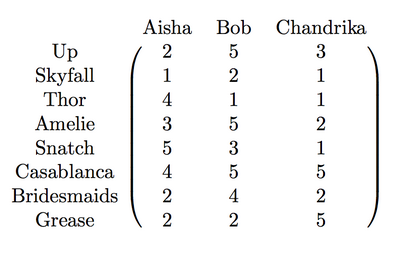
En réalité, ils sont notés sur une échelle de 1 à 5 étoiles, mais pour garder les choses simples que nous allons dire que les évaluations peuvent être des nombres réels (ils ont juste arrivé pour ramasser des entiers). Donc, cette matrice représente une carte linéaire. Le domaine est, et les vecteurs de base sont appelés personnes. et le codomaine est, dont les vecteurs base sont des films.

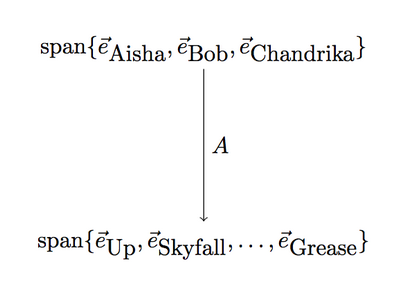
Maintenant, l'ensemble de données est représenté par, et par la définition de la façon dont une matrice représente une carte linéaire, les entires de ces vecteurs sont exactement les colonnes. Si le codomaine est vraiment grand, l'image de est un sous-espace linéaire de petite dimension de la codomain. Ceci est une étape importante, que nous avons augmenté notre point de vue à partir seulement les points de données individuels à toutes leurs combinaisons linéaires comme un sous-espace.

Bien sûr, je ne veux pas dire littéralement qu'un film (comme dans les bits comprenant un fichier contenant un film) peuvent être représentés comme une combinaison linéaire d'autres films. Je veux dire que nous pouvons représenter un film formellement comme une combinaison linéaire dans un espace abstrait vecteur pour la tâche à accomplir. Autrement dit, nous représentons les caractéristiques du film qui influent sur la note abstraitement comme vecteur. Nous n'avons pas une façon mathématique légitime de comprendre que, de sorte que le vecteur est un proxy.

Il est tout à fait clair ce que cela signifie en termes de la vie réelle, sauf que vous pouvez espérer (ou émettre l'hypothèse, ou vérifier), que si le processus de notation des films est dans la nature, alors cette représentation formelle « linéaire » reflète fidèlement le monde réel. Il est comme la façon dont les physiciens savent tous secrètement que les mathématiques ne dicte pas littéralement les lois de la nature, parce que les humains ont fait en mathématiques dans leur tête et si vous piquez la nature trop dur la casse des mathématiques vers le bas, mais il est sacrément pratique pour décrire les hypothèses (et donc sacrément précis), que nous ne pouvons pas éviter de l'utiliser pour concevoir des avions. Et nous avons rien trouvé de mieux que les mathématiques à cet effet.

De même, le classement des films ne sont pas littéralement une carte linéaire, mais si nous prétendons qu'ils sont, nous pouvons faire des algorithmes qui permettent de prédire la façon dont les films de taux de personnes assez bonne précision. Donc, si vous savez que Skyfall obtient 1,2 note et 1 de Aïcha, Bob et Chandrika, respectivement, une nouvelle personne évalueriez Skyfall basée sur une combinaison linéaire de la façon dont ils rallient à ces trois personnes. En d'autres termes, jusqu'à une combinaison linéaire, dans cet exemple Aisha, Bob, et Chandrika incarnent le processus de classement des films.

Et maintenant, nous arrivons à la clé: la matrice d'affacturage via SVD offre une alternative et de représenter plus utile au processus de personnes des films notation. En changeant la base d'un ou deux espaces vectoriels en jeu, on isole les différentes caractéristiques (orthogonales) du processus. Dans le cadre de notre exemple de film, « factorisation » signifie ce qui suit:

1. Venez avec une liste spéciale des vecteurs afin que chaque film peut être écrit comme une combinaison linéaire des.
2. Faites la chose analogue pour les personnes à obtenir.
3. Faire (1) et (2) de telle sorte que la carte est en diagonale par rapport à la fois de nouvelles bases simultanément.

On pourrait penser à la « films comme idéalisés » et les comme « critiques idéalisée. » Si vous voulez utiliser ces données pour dire des choses sur le monde, vous gagnerais l'hypothèse que toute personne peut être écrite comme une combinaison linéaire de et tout le film peut être écrit comme une combinaison linéaire des. Ce sont les lignes / colonnes de la factorisation. Pour rappel, ces combinaisons linéaires ne sont que par rapport à la tâche de classement des films. Et ils sont « spéciaux » parce qu'ils font la matrice diagonale.

1. Toutes les personnes évaluent des films via la même carte linéaire.
2. Toute personne peut être exprimé (dans le seul but de la classification des films) que des combinaisons linéaires de personnes « idéales ». De même pour les films.
3. Les films « idéalisée » et les gens peuvent être exprimés sous forme de combinaisons linéaires des films / personnes dans notre jeu de données particulier.
4. Il n'y a pas d'erreurs dans les évaluations.

On pourrait avoir une discussion profonde et intéressante sur les aspects philosophiques (ou éthiques ou culturelles) de ces hypothèses. Mais puisque l'Internet préfère regarder brûler respectueux du discours, nous allons maintenant passer à des algorithmes à la place.

approximation sous-espaces

Comment savons-nous ce n'est pas déjà rang bas? Les raisons est que les données avec même le plus minuscule peu de bruit est de plein rang avec une probabilité écrasante. Une façon concrète de dire est que l'espace des matrices de rang bas a petite dimension (dans le sens d'un collecteur) à l'intérieur de l'espace de toutes les matrices. Ainsi, même une perturbation seule entrée par une quantité infinitésimale augmenterait le rang.

On n'a pas besoin de comprendre les collecteurs pour comprendre le SVD, cependant. Pour notre exemple des personnes évaluant les films de la pleine propriété rang devrait être évident. Le bruit et le caractère aléatoire et arbitraire dans les préférences humaines détruit certainement une structure linéaire « parfaite » que nous pouvions espérer trouver, et en particulier: les données elles-mêmes définies, à savoir l'image, est un sous-espace de grande dimension de la codomain.

Trouver une approximation de rang bas peut être considéré comme « lissage » du bruit sur les données. Et cela fonctionne particulièrement bien lorsque le processus sous-jacent est proche d'une carte linéaire. Autrement dit, lorsque les données sont près d'être entièrement contenu dans un seul sous-espace de dimension relativement faible. Une façon de penser des raisons pour lesquelles cela pourrait être le cas que si le processus vous observez est vraiment linéaire, mais les données que vous obtenez est corrompu par de petites quantités de bruit. Ensuite, sera proche de rang inférieur dans un sens mesurable (à définir mathématiquement dans le poste de suite) et l'approximation de rang bas sera un substitut plus efficace, précis et généralisables pour.

En ce qui concerne notre liste précédente des hypothèses sur le moment où vous pouvez l'algèbre linéaire pour résoudre les problèmes, pour le SVD, nous pouvons ajouter « approximativement » aux trois premières hypothèses, et « pas trop d'erreurs » à la quatrième. Si ces hypothèses tiennent, SVD nous donnera une matrice qui représente avec précision le processus en cours de mesure. A l'inverse, si SVD se porte bien, alors vous avez des preuves que le processus est linéaire esque.

Ca y est, dans la mesure où la compréhension intuitivement ce que le SVD est. Je dois ajouter que la SVD ne permet pas seul à calculer une approximation de rang, il vous permet en fait de définir et d'obtenir une représentation exacte de. Nous venons de ne l'utiliser à cette fin dans cette série.

Le second bit de l'intuition est la suivante. Il est seulement un peu plus près de la rigueur, mais de toute façon ce petit aperçu SVD vraiment fait cliquer pour moi:

Le SVD est ce que vous obtenez lorsque vous résoudre itérativement le problème d'optimisation avide de données d'ajustement à une ligne.

Je veux dire, vous pouvez calculer le SVD en procédant comme suit:

1. Quelle est la meilleure ligne de pose mes données?
2. D'accord, en ignorant que la première ligne, ce qui est la meilleure ligne?
3. D'accord, en ignorant toutes les lignes dans l'espace de ces deux premières lignes, ce qui est la meilleure ligne?
4. Ignorant toutes les lignes en l'espace des trois premières lignes, ce qui est la meilleure ligne?
5. (répéter)

Il devrait être choquant que cela fonctionne. Pour la plupart des problèmes, en mathématiques et dans la vie, l'algorithme glouton est loin d'être optimale. Quand il arrive, une fois par lune bleue, que l'algorithme glouton est la meilleure solution à un problème naturel (et évidemment pas ainsi, ou tout simplement à peu près donc), il est de notre devoir intellectuel d'arrêter ce que nous faisons, se tenir droit, et vraiment comprendre et apprécier. Ces merveilles transcendent les querelles politiques et les résultats sportifs. Et nous allons commencer le prochain billet immédiatement en plongeant dans ce problème avide d'optimisation.

Le point de vue géométrique

Pour moi, la clé qui manque de cette explication est l'accent mis sur l'approximation. Ce qui rend le SVD si magique n'est pas que la factorisation existe en premier lieu, mais plutôt que le SVD a ces couches de plus en plus bonne approximation. Bien que la terminologie viendra dans le prochain post, ces couches sont les (ordonnées) vecteurs singuliers et valeurs singulières. Et d'ailleurs, que le processus algorithmique de la construction de ces couches va nécessairement dans l'ordre de l'approximation la plus forte à la plus faible.

La prochaine fois: algorithmes

La prochaine fois que nous allons connecter tout cela aux définitions formelles et rigueur. Nous allons étudier l'approche algorithme glouton, puis nous allons mettre en œuvre le SVD et le tester sur certaines données.

Je pense que la transformation n'est pas affines? Il n'y a pas de traduction, juste rotation et mise à l'échelle.

Chaque espace linéaire induit une classe d'espaces affines. En particulier, envisager l'intersection des plans passant par une origine d'un plan légèrement décalé par rapport à l'origine.

Une question sur « rang plein » - la matrice A est 8 × 3 est donc pas son lin # maximale ind. des lignes ou des colonnes 3? Est-ce que plein rang signifie que ce maximum ou quelque chose de plus - par exemple, s'il y a 1000 films et encore 3 personnes il y a un espace R ^ 3 personnes, mais l'espace R ^ 1000 des films avec un sous-espace R ^ 3 des combos linéaires en elle? Merci pour le post sur le blog!

Si par exemple vous avez seulement trois colonnes et que vous voulez utiliser SVD, votre univers doit être en 3 dimensions. Par exemple, un chef peut utiliser des ingrédients sous forme de colonnes, mais vous avez besoin d'un grand nombre d'alors pour créer un plat délicieux. Ce que je veux souligner est que vos lignes et les colonnes doivent être assez grand pour décrire l'univers du discours, l'opinion générale ou être en mesure d'être utilisé pour l'approximation de la réalité que vous modélisez. Alors qu'est-ce SVD vous donne est une base spéciale, un groupe de chefs capables de concevoir la saveur que vous voulez. Je pense que la motivation devrait être le long de ces lignes, la première question de la puissance expressive de votre base.

SVD peut illustrer le concept de « rang » d'une manière vraiment cool: comme l'entropie.

1) créer une matrice 20 x 100 de nombres aléatoires
2) exécuter SVD. Les valeurs singulières devraient être 20 nombres presque exactement égaux.
3) multiplier la matrice par elle-même pour créer une matrice de 100 x 100
4) exécuter SVD sur ce

Vous devriez obtenir un vecteur singulier avec 20 valeurs qui sont presque exactement les mêmes et 80 valeurs qui sont infitesimally petites. Votre 20 x matrice 100 a rang presque maximale. Votre 100 × 100 matrice a seulement 20 x 100 valeur de rang, gonflé comme un ballon.

Rang de l'entropie.

Je cherchais un article comme celui-ci pour un certain temps maintenant, cela est tellement aide, merci!
Cependant, j'ai un mal à saisir comment interpréter certains ensembles de données sous forme de cartes linéaires. Par exemple:
1) Comment interprétez-vous une image numérique représentée par une matrice comme linéaire?
2) Comment interprétez-vous une matrice de données dont la ligne et le numéro de colonne représentent des indices de la position (x_i, y_k) et l'élément de matrice comme la valeur qu'il faut y? M_ik = f (x_i, y_k)

Dans une certaine mesure, les deux réponses à votre question sont tout simplement « de la même façon que vous interprétez une matrice comme linéaire, » qui est en ayant un vecteur de base pour chaque ligne / colonne et chaque colonne d'entrées indexées par un vecteur de base exprime la expansion de la forme d'une combinaison linéaire des vecteurs de base de la ligne.

Ce n'est pas une réponse « agréable » pour vos deux exemples parce que le choix des vecteurs de base pour le domaine et codomaine sont inventées. Mais, par exemple pour des images, c'est juste comment le monde fonctionne. La représentation standard est pas très utile pour l'algèbre linéaire. Donc, les gens vont sur les études comment choisir une meilleure base, et ils finissent avec des choses comme la transformée de Fourier et tout ce beau genre de choses. Je pense qu'une grande partie de l'applicabilité de l'algèbre linéaire dépend de la façon dont les choix arbitraires ont été que vous avez obtenu vos données en premier lieu.

Laisser un commentaire Annuler la réponse

écrire du code, les lettres couvre pas
application commune de Triplebyte permet aux programmeurs de talent sauter les écrans de curriculum vitae et recruteur tout en appliquant à plusieurs reprises dans les entreprises de haute technologie à la fois. Battre leur quiz en ligne de codage pour commencer. Les personnes intéressées par les mathématiques et la physique ont tendance à bien faire.

Articles Liés

• décomposition et analyse principale composante valeur Singulier

• MATH2071 LAB 9 La Décomposition en Valeurs Singulières

• tutoriel de décomposition Singular Value (SVD)