3 façons de résoudre un carré magique

Les carrés magiques ont gagné en popularité avec l'avènement des jeux basés sur les mathématiques comme Sudoku-. Un carré magique est un ensemble de nombres dans un carré de telle sorte que la somme de chaque rangée, colonne et diagonale est un nombre constant, que l'on appelle « constante magique ». Cet article va vous dire comment résoudre tout type de carré magique, que ce soit un numéro impair, seul paire, ou double-paires.

Modifier étapes

Méthode L'un des trois:
Résolution d'un carré magique-Odd Edition Numérotée

Calculer la constante magique. [1] Vous pouvez trouver ce numéro en utilisant une formule mathématique simple, où n = le nombre de lignes ou des colonnes dans votre carré magique. Ainsi, par exemple, dans un carré magique 3x3, n = 3. La magie constante n = [(n ^ 2 + 1) / 2]. Ainsi, dans l'exemple de la place 3x3:

• somme = 3 * [(9 + 1) / 2]
• somme = 3 * (10/2)
• somme = 3 * (5)
• somme = 15
• La constante magique pour un carré 3x3 est 15.
• Toutes les lignes, les colonnes et les diagonales doivent ajouter à ce nombre.

Placer le numéro 1 dans la zone centrale de la rangée supérieure. C'est toujours là où vous commencez quand votre carré magique a des côtés impairs, quel que soit grand ou petit ce nombre est. Donc, si vous avez un carré 3x3, placez le numéro 1 dans l'encadré 2; dans un carré de 15x15, placez le numéro 1 dans la case 8.

Remplissez les numéros restants à l'aide d'un haut-un, droit un motif. Vous aurez toujours remplir les numéros de séquence (1, 2, 3, 4, etc.) en se hissant une ligne, une colonne à droite. Vous remarquerez immédiatement que pour placer le numéro 2, vous passerez au-dessus de la rangée supérieure, de la place magique. C'est correct - même si vous travaillez toujours dans ce haut-un, droit d'une manière, il y a trois exceptions qui ont également modelés, des règles prévisibles:

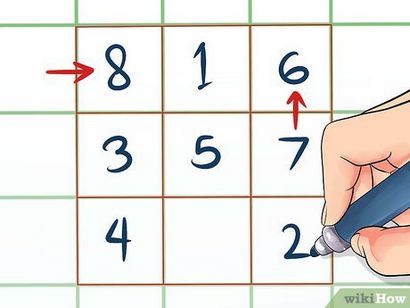
• Si le mouvement vous amène à une « boîte » au-dessus de la rangée supérieure de carré magique, rester dans la colonne de cette boîte, mais placer le numéro dans la rangée du bas de cette colonne.
• Si le mouvement vous amène à une « boîte » à droite de la colonne de droite du carré magique, rester dans la ligne de cette boîte, mais placer le numéro dans la plus colonne de gauche de cette ligne.
• Si le mouvement vous amène à une boîte qui est déjà occupé, revenir à la dernière case qui a été remplie et placez le numéro suivant directement en dessous.

Méthode Deux des trois:
Résoudre un Singly Même carré magique Modifier

Comprendre ce qu'est un seul carré est même. Tout le monde sait qu'un nombre pair est divisible par 2, mais dans des carrés magiques, il existe différentes méthodes pour résoudre simple et double même carrés.

• Un seul même carré a un certain nombre de boîtes de chaque côté qui est divisible par deux, mais pas 4. [2]
• Le plus petit possible carré seul même magie est 6x6, car les places 2x2 magiques ne peuvent être faites.

Calculer la constante magique. Utiliser la même méthode comme avec les carrés magiques impairs: la magie constante = [n * (n ^ 2 + 1)] / 2, où n = le nombre de boîtes de chaque côté. Ainsi, dans l'exemple d'un carré de 6x6:

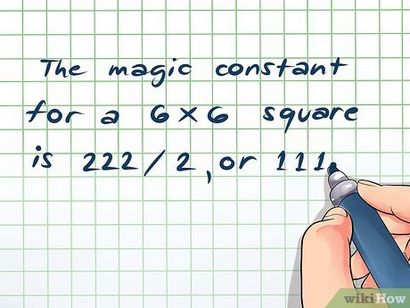
• = somme [6 * (62 + 1)] / 2
• = somme [6 * (36 + 1)] / 2
• somme = (6 * 37) / 2
• somme = 222/2
• La constante magique pour un carré de 6x6 est 222/2 ou 111.
• Toutes les lignes, les colonnes et les diagonales doivent ajouter à ce nombre.

Diviser le carré magique en quatre quadrants de taille égale. les étiqueter A (en haut à gauche), C (en haut à droite), D (en bas à gauche) et B (en bas à droite). Pour comprendre la taille de chaque carré doit être, il suffit de diviser le nombre de boîtes dans chaque ligne ou colonne de moitié.

• Ainsi, pour un carré de 6x6, chaque quadrant serait boîtes 3x3.

Attribuer à chaque quadrant un ensemble de nombres. Quadrant A obtient pour le quart de l'effectif; Quadrant B au deuxième trimestre; Quadrant C au troisième trimestre, et Quadrant D le dernier trimestre de la plage de nombre total pour la place magique 6x6.

• Dans l'exemple d'un carré de 6x6, Quadrant A serait résolu avec les nombres de 1 à 9; Quadrant B avec 10-18; Quadrant C avec 19-27; et le quadrant D avec 28-36.

Résoudre chaque quadrant en utilisant la méthode de carrés magiques impaires. Quadrant A sera simple à remplir, car il commence par le numéro 1, comme des carrés magiques font habituellement. Quadrants B-D, cependant, va commencer avec des chiffres étranges - 10, 19 et 28, respectivement, dans notre exemple.

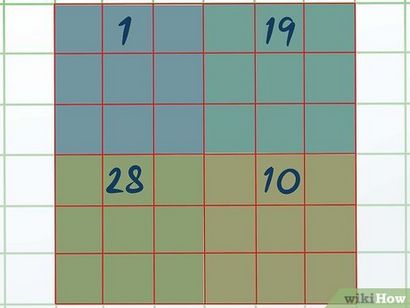
• Traiter le premier numéro de chaque quadrant comme si elle est le numéro un. Placez-le dans la zone centrale sur la rangée supérieure de chaque quadrant.
• Traiter chaque quadrant comme son propre carré magique. Même si une boîte est disponible dans un quadrant adjacent, l'ignorer et de sauter à la règle « d'exception » qui correspond à votre situation.

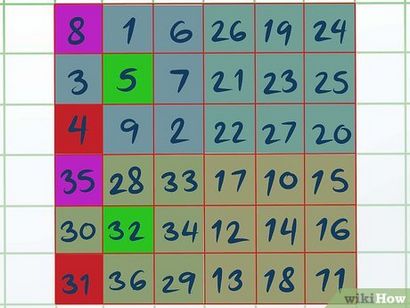
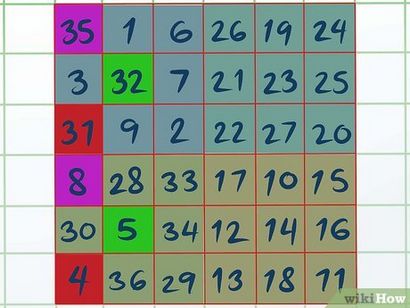
Swap Faits saillants A et D. Ceci est un à un échange; il suffit de soulever et de remplacer les boîtes entre Quadrant A et Quadrant D sans changer leur ordre du tout. Une fois que vous avez fait cela, toutes les lignes, colonnes et diagonales dans votre carré magique devrait ajouter à la constante magique que vous avez calculé.

Faire un échange supplémentaire pour les places seules, même magiques de plus de 6x6. En plus de l'échange pour les quarts de cercle A - D mentionné ci-dessus, vous devez également faire un échange de quarts de cercle C - B. Mettre en évidence les colonnes du côté droit de la place vers la gauche un de moins que le nombre de colonnes en surbrillance pour A- moment fort 1. Permuter les valeurs dans le quadrant C avec les valeurs de quadrant B pour ces colonnes, en utilisant le même one-to-one procédé.

• Voici deux images d'un carré magique 14x14 avant et après avoir fait les deux swaps. Quadrant Une zone d'échange est mis en surbrillance bleue, zone de swap Quadrant D est en surbrillance verte, zone de swap Quadrant C est surligné en jaune, et la zone de swap Quadrant B est mis en surbrillance orange.
  • 14x14 carré magique avant de swap (étapes 6, 7, - 8)
  
  

• 14x14 carré magique après avoir fait swap (étapes 6, 7, - 8)
  
  

  Comment puis-je résoudre un carré magique avec les mêmes nombres entiers positifs et négatifs?

  Répondu par wikiHow Contributeur

  • Pour résoudre un carré magique avec les mêmes nombres entiers positifs et négatifs, remplacer le problème que vous ne savez pas comment résoudre avec celui que vous ne savez comment résoudre. En d'autres termes, remplacer les entiers avec les n premiers entiers positifs, où n est le nombre d'entiers. Résoudre le carré, remplacez les entiers avec les entiers d'origine dans le problème que vous avez reçus. Donc, si elle est un carré 3x3 avec des nombres entiers de -4 à 4, le transformer en un carré régulier de 3x3, le résoudre, et remplacer 1 dans la solution finale à -4, remplacer 2 à -3, -2 remplacer avec 3, etc. .

  Comment puis-je résoudre un carré de 3 x 3 magique en utilisant les nombres pairs?

  Répondu par wikiHow Contributeur

  • Dans un carré magique normal, vous avez les numéros 1 à 9. Pour les rendre encore des chiffres, il suffit de multiplier chaque nombre par 2.

  Comment puis-je résoudre un carré magique en utilisant des nombres négatifs?

  Répondu par wikiHow Contributeur

  • Il est le même que tout autre problème de mathématiques. Toutes les horizontales, diagonales - lignes verticales doivent ajouter au même numéro. L'ajout d'un nombre négatif pour un nombre positif est le même que la soustraction et l'addition d'un nombre négatif pour un nombre négatif est le même que l'ajout des nombres positifs, à l'exception que la réponse est négative. Si tous les numéros dans l'exemple carré magique ont été négatifs, la réponse pour chaque équation serait -34.

  Y at-il une autre solution qui garantit que toutes les solutions sont trouvées? Par exemple, il y a plus d'une façon de résoudre le 6 x 6 carrés.

  Répondu par wikiHow Contributeur

  • Il est un problème ouvert en mathématiques - en fait, pour des places plus grandes que 6 x 6, il même une formule comptant combien il existe de nombreux carrés magiques est pas.

  Comment puis-je résoudre un carré de 3 x 3 magique en utilisant 72-80?

  Répondu par wikiHow Contributeur

  • Il suffit de prendre toute 3 x 3 carré magique avec 1 - 9 (nombre magique 15), et à 71 à chaque cellule.

  Est un carré magique ou d'un rectangle de 5 x 6 possible de le faire?

  Répondu par wikiHow Contributeur

  • Vous ne pouvez pas faire les sommes des lignes égales les sommes de colonne à moins que le tableau est carré.

  Comment puis-je créer un 6 * 6 boîte magique?

  Articles Liés

  • Carré magique

  • 3 façons simples de simplifier une racine carrée (avec photos)

  • 3 façons de trouver une racine carrée sans calculatrice