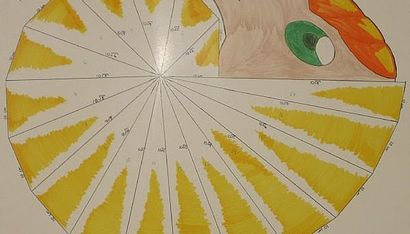
Comment faire une spirale du théorème de Pythagore, sciencing

Un examen rapide du théorème
Le théorème de Pythagore stipule que, dans un triangle rectangle, le carré de l'hypoténuse est égal au carré des deux autres côtés. Exprimé mathématiquement, cela signifie que A + B au carré au carré = C carré. Tant que vous connaissez les valeurs pour les deux côtés d'un triangle rectangle, vous pouvez utiliser ce calcul pour arriver à une valeur pour le troisième côté. L'unité de mesure réelle que vous choisissez d'utiliser pourrait être quelque chose de pouces à miles, mais la relation reste le même. C'est important de se rappeler que vous ne travaillerez pas toujours nécessairement une mesure physique spécifique. Vous pouvez définir une ligne d'une longueur « 1 » à des fins de calcul, puis exprimer toute autre ligne par sa relation avec votre unité choisie. C'est ainsi que la spirale fonctionne.
A partir de la spirale
Pour construire une spirale, faire un angle droit avec les côtés A et B de longueur égale, qui devient la valeur « 1 ». Ensuite, faire un autre triangle en utilisant côté C de votre premier triangle - l'hypoténuse - comme la face A du nouveau triangle. Maintenir le côté B de la même longueur à votre valeur choisie de 1. Répéter à nouveau le même procédé, en utilisant l'hypoténuse du second triangle comme le premier côté du nouveau triangle. Il faut 16 triangles à venir tout autour du point où la spirale commencerait à se chevaucher votre point de départ, ce qui est là ancien mathématicien Theodorus arrêté.
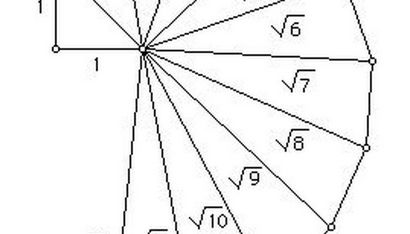
Racine carrée Spirale
Le théorème de Pythagore nous dit que l'hypoténuse du premier triangle doit être la racine carrée de 2, parce que chaque côté a une valeur de 1 et 1 au carré est toujours 1. Par conséquent, chaque côté a une superficie de 1 carré, et quand ceux-ci sont ajoutés le résultat est 2 au carré. Ce qui rend la spirale intéressante est que l'hypoténuse du triangle suivant est la racine carrée de 3, et celle d'après est la racine carrée de 4, et ainsi de suite. C'est pourquoi il est souvent désigné comme une spirale de racine carrée, plutôt que d'une spirale pythagoricienne ou en spirale Theodorus. Sur le plan pratique, si vous avez l'intention de créer une spirale en tirant sur papier ou en coupant des triangles de papier et de les monter sur un support en carton, vous pouvez calculer à l'avance la taille de votre valeur de 1 peut être si la spirale fini est pour tenir sur la page. Votre ligne la plus longue sera la racine carrée de 17, pour quelle que soit la valeur 1 que vous avez choisi. Vous pouvez travailler en arrière à partir de la taille de votre page pour trouver une valeur appropriée de 1.