Expressions Algébriques distributivité
Supposons que nous ayons 3 paniers, contenant chacune 2 pommes et 4 oranges.

Ceci est le même nombre de pommes et des oranges comme si nous avions un sac avec 6 pommes et un sac avec 12 oranges. Sauf que nous mystérieusement n'avons plus nos trois paniers qui ont été faits à la main à Santa Fe et maintenez en fait un peu de valeur sentimentale pour nous. C'est une honte.
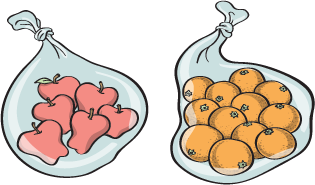
Peu importe la façon dont nous les emballons, le nombre de fruits reste le même. Non pas que cela enlève la piqûre d'avoir eu nos récipients en osier volés juste sous notre nez.
Ceci est un exemple de la propriété distributive. qui dit essentiellement que peu importe la façon dont nous les numéros « paquet » lors de l'exécution multiplication. Pour écrire la propriété distributive des symboles, nous disons que si a, b. et c sont des nombres réels, alors:
problème échantillon
Maintenant, la chose que nous distribuons est 3x. plutôt que d'un nombre bon vieux tout par son lonesome. C'est bien, parce que la propriété distributive fonctionne toujours.
Rappelez-vous comment fonctionne la notation exposant? Dans le cas contraire, une remise à niveau ici. Si nous distribuons quelque chose qui a une variable sur une quantité entre parenthèses qui contient également cette variable, nous utilisons la notation exposant pour garder les choses en ordre. Ne pourrait probablement pas faire du mal à pulvériser aussi vers le bas avec quelques giclées de verre Plus. Utilisons exposants pour terminer.
problème échantillon
problème échantillon
Ayant un signe négatif par lui-même à l'extérieur des parenthèses est le même que d'avoir -1 à l'extérieur des parenthèses. La figure 1 est là; il est juste cacher. Avez-vous vérifié sous le lit? C'est tout à fait son endroit préféré. Pour distribuer le signe négatif, vous simplement multiplier chaque terme dans les parenthèses par -1.
problème échantillon
Quelle est la version élargie de - (2a - 5b - 6 + 11c)?
Il suffit de multiplier terme tous les puants dans les parenthèses par -1.
Soit dit en passant, puisque la multiplication est commutative, la propriété distributive fonctionne également si nous écrivons la multiplication dans l'autre sens:
problème échantillon
Utiliser la distributivité pour multiplier (4x - y) (- 3).
Ceci est la même chose que -3 (4x - y), de sorte que multiplier -3 par les termes et le tour est joué:
problème échantillon
Utiliser la distributivité pour multiplier (4 - x) (- 1).
Même vieux. Virer de bord -1 sur les deux termes.
Prêt à être vraiment aux affaires? La propriété distributive fonctionne toujours, même si l'expression entre parenthèses a plus de deux mandats. Il est tout à fait un joueur d'équipe.
problème échantillon
Quelle est la version élargie de 4 (x + y + z)?
Celui-ci est pas trop mal. Gifler un 4 sur chaque variable et nous avons terminé.
La propriété distributive fonctionne également lorsque nous multiplions les expressions où les deux facteurs ont plusieurs termes. Donc, si vous êtes un joueur de tennis, il est un peu comme jouer en double droite plutôt que de doubles canadiens. Ou triplets. D'accord, l'analogie tombe en quelque sorte en dehors à ce moment. nous ignorer et jeter un oeil à un exemple.
problème échantillon
Bon, pour ce que nous allons utiliser deux fois la propriété distributive. Il est temps double distribution. Fondamentalement, nous voulons continuer à distributin' jusqu'à ce que le jour se fait. Ou du moins jusqu'à ce qu'il n'y a plus rien à distribuer.
D'abord, nous séparer les 3 et le x dans le premier facteur.
Ensuite, nous distribuons les deux termes séparément comme normal.
L'homme, qui a beaucoup de choses à garder une trace de coup. Pensez combien il serait plus facile si vous pouviez prendre une douche, se brosser les dents, manger le petit déjeuner, et vous habiller tout en même temps. Quel gain de vie qui serait! Surtout le matin que l'alarme ne se déclenche.