Ogive, Math @
La branche des mathématiques qui traite avec une grande quantité de données numériques, est connu comme statistique. Il est une science de la collecte, tabuler, l'organisation, le calcul et l'interprétation des données statistiques. Les méthodes statistiques sont couramment utilisés dans les recherches et les enquêtes où de vastes données sont utilisées. En général, les statistiques requièrent différents types de graphiques afin de mieux comprendre les données. Les graphiques les plus utilisés sont graphique à barres, histogramme, polygone de fréquence, la ligne graphique, la courbe de fréquence cumulée, etc.
Le mot Ogive est essentiellement un terme utilisé dans l'architecture pour décrire des courbes ou des formes courbes. Ogives sont des graphiques qui sont utilisés pour estimer le nombre de numéros se trouvent ci-dessous ou au-dessus d'une variable ou une valeur particulière dans les données. Afin de construire ogive, d'abord la fréquence cumulée des variables est calculée en utilisant une table de fréquences. Il se fait en ajoutant les fréquences de toutes les variables précédentes dans l'ensemble de données. Le résultat ou le dernier numéro dans le tableau de fréquence cumulée est toujours égale à la fréquence totale des variables.
ogive Définition
Ogive est un graphique d'une distribution cumulative, qui montre des valeurs de données sur l'axe horizontal et soit les fréquences cumulées, les fréquences relatives cumulées ou des fréquences cumulées en pourcentage sur l'axe vertical. La Ogive est construite en traçant un point correspondant à la fréquence cumulée de chaque classe.
Les graphiques les plus utilisés de la distribution de fréquences sont les suivantes:- histogramme
- polygone de fréquence
- Courbe de fréquence
- Ogives (courbes de fréquence cumulée)
Graphique ogive
Un graphique Ogive est une courbe de la distribution de fréquence cumulative ou fréquence relative cumulée distribution.To tirage d'une telle courbe, tout d'abord la fréquence simple doit être exprimée en pourcentage de la fréquence totale. Ensuite, ces pourcentages sont cumulés et reportés comme dans le cas d'un ogivale.
fréquence Ogive
Il y a deux façons de construire une courbe de fréquence cumulée ou ogivale. Les étapes de la construction de moins de tableau Ogive et plus de tableau Ogive sont donnés ci-dessous:
Étapes à suivre pour la construction d'un tableau moins Ogive (moins de courbe de fréquence cumulée):
- Dessiner et étiqueter les axes horizontaux et verticaux.
- Prendre les fréquences cumulées le long de l'axe y (axe vertical) et les limites de la classe supérieure sur l'axe des x (axe horizontal)
- Tracer les fréquences cumulées contre chaque limite de classe supérieure.
- Joignez-vous aux points avec une courbe lisse.
Voyons avec l'aide d'une table comment construire un « moins » Tableau Ogive:
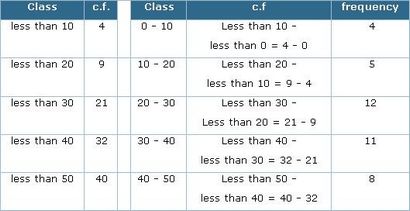
Lorsque nous écrivons, « moins de 10 - moins de 0 », la différence donne la fréquence 4 pour l'intervalle de classe (0 - 10) et ainsi de suite.
Procédure pour la construction d'un plus grand que ou plus de diagramme Ogive (plus de courbe de fréquence cumulée):- Dessiner et étiqueter les axes horizontaux et verticaux.
- Prendre les fréquences cumulées le long de l'axe y (axe vertical) et les limites de la classe inférieure sur l'axe des x (axe horizontal)
- Tracer les fréquences cumulées contre chaque limite de classe inférieure.
- Joignez-vous aux points avec une courbe lisse.
Voyons avec l'aide d'une table comment construire un « plus » Tableau Ogive:
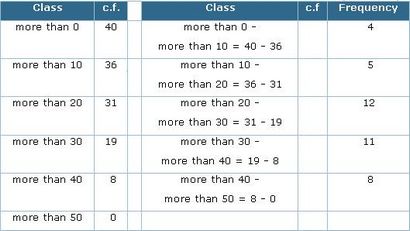
Quand nous écrivons « plus de 0 - plus de 10 », la différence donne la fréquence 4 pour l'intervalle de classe (0 - 10) et ainsi de suite.
Correspondant au point d'intersection est inférieure à la courbe de fréquence cumulée, supérieure ou plus de la courbe de fréquence cumulée est la médiane de la distribution. Ainsi, nous pouvons trouver la valeur middlemost de la série si nous tirons moins et supérieur à Ogives.
résolu Exemple
Question: Dessiner plus que la courbe de fréquence cumulée pour les données suivantes